Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.2 - Ex. 14

A Figura mostra a leitura de um monitor de pressão montado em um ponto da trajetória de uma onda sonora de uma só frequência, propagando-se a 343   m / s em um ar de massa específica homogênea 1,21   k g / m 3 . A escala do eixo vertical é definida por Δ p s = 4,0   m P a . Se a função deslocamento da onda é s ( x ,   t )   =   s   c o s ( k x   - ω t ) , determine (a) s m , (b) k   e (c) ω . Quando o ar é resfriado, a massa específica aumenta para 1 1,35   k g / m 3 e a velocidade da onda sonora diminui para 320   m / s . A fonte emite uma onda com a mesma frequência e a mesma pressão que antes. Qual é o novo valor (d) de s m , (e) de k e (f) de ω ?

Passo 1

(a)Show de bolinhas galerinha, o primeiro passo importante para respondermos essa questão é observarmos o que nos mostra a figura.

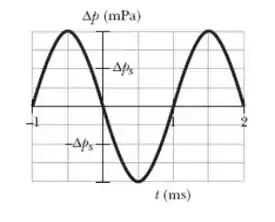
A primeira coisa que nos chama atenção nela são os valores do período T e da amplitude da onda. O período é o intervalo de tempo entre duas posições equivalentes consecutivas, como por exemplo duas cristas da onda. Podemos ver na figura que ele é igual a T = 2,0   ms . Além disso, a amplitude dessa onda é igual a:

Δ p s = 4,0   mPa

Além disso, precisamos agora lembrar de um resultado muito importante relacionado à amplitude de pressão de uma onda sonora. Tudo parte da definição do módulo de elasticidade de um gás B . Ele é igual a:

B = - Δ p Δ V V

B = v ² ρ

Tal que v e ρ são a velocidade de propagação do som no gás e a sua densidade. Além disso, sendo V = A × Δ x o volume de um elemento de gás, como o representado na figura abaixo, e Δ V = A × Δ s a variação de volume, temos que:

Δ p = - B Δ s Δ x

∆ p = - B ∂ s ∂ x

∆ p = - B ∂ s m cos ⁡ k x - ω t ∂ x

Logo:

∆ p = B k s m s e n ( k x - ω t )

Pronto! Desenvolvemos isso para mostrar que a amplitude de pressão (valor numérico que multiplica a expressão do seno acima) vale B k s m . Como B = v ² × ρ , temos que essa amplitude é igual a :

Δ p m = v 2 ρ k s m

Passo 2

Iradoso, como mostra nossa figura da questão, Δ p m = 2 × Δ p s = 8,0   mPa . Jogando esse valor na expressão

Δ p m = v 2 ρ k s m

∆ p m = v ρ v × k s m

∆ p m = v ρ ω s m

Temos:

8,0   mPa = 343   m/s   1,21 kg/m³ 2 π 2,0   ms s m

Então isolando s m , obtemos que:

s m ≅ 6,1 × 10 - 9   m

Passo 3

(b)O número de onda k vale:

k = ω v

k = 2 π T v

Logo:

k ≅ 9,2   rad/m

Passo 4

(c)A freqüência angular é dada por

ω = 2 π T

ω ≅ 3142   rad/s

Ou:

ω = 3,1 × 10 3   s -1

Passo 5

(d)Para calcularmos s m correspondente à densidade de ρ ' = 1,35  kg/m³ e à velocidade v = 320   m/s , basta substituirmos esses valores nas equações que achamos acima:

s m = Δ p m v ' ρ ' ω

s m = Δ p m v ' ρ ' 2 π T

s m = 5,9 × 10 - 9   m

Ou em nm :

s m = 5,9   nm

Passo 6

(e) O número de onda é igual a :

k = 2 π λ

k = ω v '

Logo:

k ≅ 9,8   rad/m

Passo 7

(f)A freqüência angular é igual a:

ω = 2 π T

ω ≅ 3142   rad/s

Ou:

ω = 3,1 × 10 3   s -1

Resposta

  1. 6,1 × 10 - 9   m
  2. 9,2   rad/m
  3. 3,1 × 10 3   s -1
  4. 5,9   nm
  5. 9,8   rad/m
  6. 3,1 × 10 3   s -1
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois espectadores de uma partida de futebol no estádio de Montjuic veem e depois ouvem uma bola ser chutada no campo. O tempo de retardo para o espectador A é 0,23s e para o espectador B é 0,12s . As
Uma coluna de soldados, marchando a 120 passos por minuto, segue o ritmo da batida de um tambor que é tocado na frente da coluna. Observa-se que os últimos soldados da coluna estão levantando o pé esq
Quando a porta da Capela do Mausoléu, em Hamilton, Escócia, é fechada, o último eco ouvido por uma pessoa que está atrás da porta, no interior da capela, ocorre 15s depois. (a) Se esseeco se devesse a
Quando a porta da Capela do Mausoléu, em Hamilton, Escócia, é fechada, o último eco ouvido por uma pessoa que está atrás da porta, no interior da capela, ocorre 15s depois. (a) Se esseeco se devesse a
Qual é o modulo de elasticidade volumétrico do oxigênio se 32g de oxigênio ocupam 22,4L e a velocidade do som no oxigênio é 317m / s ?