Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 37
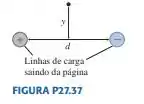
A FIGURA P27.37 mostra uma secção transversal de duas linhas de carga infinitas que se estendem perpendicularmente para fora da página. As densidades lineares de carga são
- Obtenha uma expressão para a intensidade do campo elétrico E a uma altura y acima do ponto equidistante entre as linhas.
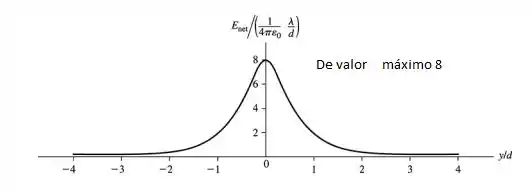
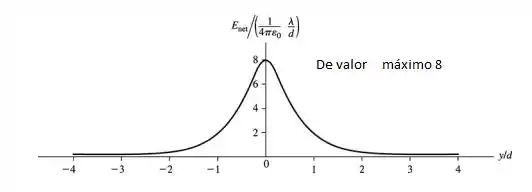
- Desenhe um gráfico de
Passo 1
Faaaaaala, galera... Tranquileba??
Primeiro temos que saber o campo elétrico em um fio longo, vamos lá?!
Se fazemos para um bastão e depois levarmos seu comprimento ao infinito, será muito mais fácil. Assim, seja um bastão:
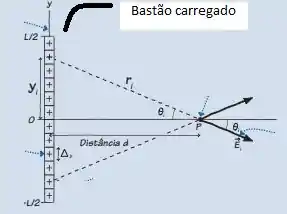
Vemos que as componentes em y se cancelam, sobrando somente em x, de forma que:
Sabemos que o campo elétrico é dado por:
Assim:
Pela imagem, vemos que:
E que:
Assim:
E ficando:
E sabemos que a densidade linear de carga é:
Logo:
Vemos na imagem que
Assim ficamos com:
Integrando sabendo que
Façamos:
Logo:
E quando:
E:
Assim ficando:
Sabemos que:
Sabemos que:
Agora, façamos esse bastão ser infinito, ou seja,
Sabemos que:
Agora que obtemos o campo elétrico, fica mais fácil de nós acharmos a resposta. Bora pro próximo passo?!
Passo 2
Assim, tendo que :
Veja que são iguais, mas colocamos dessa forma que será melhor vista em breve.
Temos então que:
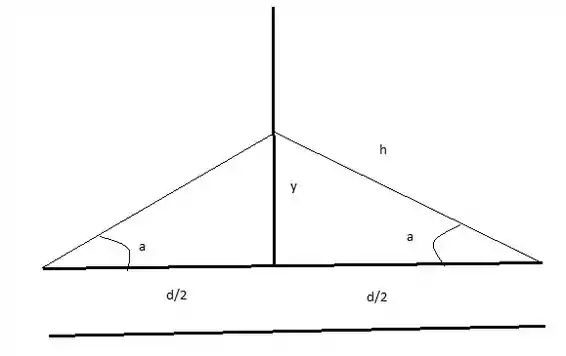
Veja que:
E:
E para o campo da esquerda:
E da direita:
De forma que o campo total seja:
E seu modulo é:
Passo 3
Para b)
Fazendo um gráfico de em unidade de d, assim temos a tabela e respectivamente seu gráfico:
Resposta
Para a)
Para b)
