Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 3

Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos de P sobre o plano. Mostre que a região do plano situada a uma distância ≤ 2 D do ponto P é responsável pela metade ( E / 2 ) do campo em P .

Passo 1

Se liga! Primeiro vamos pensar que esse plano é parecido com um disco de raio r, blz?Em seguida, vamos ver o esquema no desenho a seguir.

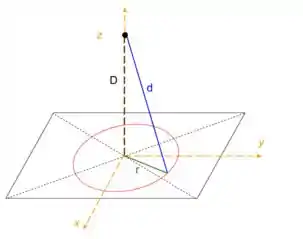
Lembre-se que podemos escrever

σ = d q d A   ⟹ d q = σ   d A e que pela figura podemos escrever que

d A = 2 π r   d r     .

Passo 2

Podemos ver na figura que

d = D 2 + r 2

e que

cos ⁡ θ = D D 2 + r 2

Passo 3

Agora podemos escrever o campo elétrico produzido por um elemento infinitesimal de carga

d E = k d q d 2 = k σ   d A D 2 + r 2 =   k σ   2 π r   d r D 2 + r 2  

Para saber a força produzida por todo o disco precisamos integrar e 0 ≤ r ≤ R . Mas, pela simetria do sistema, podemos perceber que só teremos campo apontando na direção z . Portanto, usaremos apenas a componente z do campo

E =   ∫ 0 R k σ   2 π r   d r D 2 + r 2 c o s θ = k σ 2 π ∫ 0 R r   d r D 2 + r 2 D D 2 + r 2 =   k σ 2 π D ∫ 0 R r   d r D 2 + r 2 3 / 2  

Passo 4

Só precisamos resolver a integral. Para isso, usaremos a seguinte substituição

u = D 2 + r 2 ⇒ d u = 2 r d r

Reescrevendo a integral temos

∫ 0 R r   d r D 2 + r 2 3 / 2   = 1 2 ∫ D 2 D 2 + R 2 d u u 3 / 2  

Agora parece que ficou mais simples, né?! Temos que resolver a integral deste polinômio! ∫ d u u 3 / 2   =   - 2 1 u + C

Portando substituindo o intervalo de integração teremos que

∫ 0 R r   d r D 2 + r 2 3 / 2   = 1 2 - 2 1 D 2 + R 2 - 1 D = 1 D - 1 D 2 + R 2  

Lembra que a expressão inteira era

E =   k σ 2 π D ∫ 0 R r   d r D 2 + r 2 3 / 2  

Substituindo o resultado da integral teremos

E =   k σ 2 π D 1 D - 1 D 2 + R 2 = k σ 2 π 1 - 1 1 + R 2 D 2

Substituindo

k = 1 4   π ϵ 0

Temos

E = σ 2 ϵ 0 1 - 1 1 + R 2 D 2

Podemos verificar que quando R → ∞ , o campo passa a ser

E = σ 2 ϵ 0

Como teremos que verificar ainda outra condição, chamaremos este campo de E 1 .

Passo 5

Podemos ver que d ≤ 2 D

R → D 3

Nessas condições, substituindo esse valor no lugar de R na expressão obtida para o campo, temos

E 2 = σ 4 ϵ 0

Fazendo a razão

E 1 E 2 = σ 2 ϵ 0 σ 4 ϵ 0 ⇒ E 2 = E 1 2       .

Pronto! Acamos de mostrar o que ele pediu!

Resposta

E 2 = E 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitas linhas retas de carga.
Uma linha de cargas com densidade linear uniforme λ está ao longo do eixo x desde x = x 1 até x = x 2 , onde x 1x 2 . Mostre que a componente x do campo elétrico em um ponto no eixo y é dado por E x =
Uma linha infinitamente longa de cargas tem densidade linear uniforme igual a - 1,50μ C / m e é paralelo ao eixo y em x = - 2,00m Uma crga puntiforme positiva igual a a 1,30μ C está localizada em x =
Uma fina lâmina infinita no plano y = 0 tem densidade superficial de carga σ 1 = + 65n C / m 2 . Uma segunda fina lâmina infinita tem densidade uniforme de carga σ 2 = + 45n C / m 2 , intercepta o pla
Uma linha infinitamente longa uniformemente carregada com carga negativa, tem densidade linear de carga igual a λ e está localizada no eixo z . Uma pequena partícula carregada positivamente tem massa