Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 11.Problemas - Ex. 46
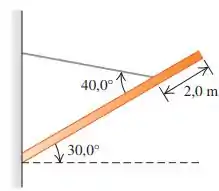
Uma viga uniforme de 8,0 m e massa de 1.150 kg está presa por uma dobradiça a uma parede e sustentada por um cabo delgado preso a 2,0 m da extremidade livre da viga (Figura P11.46). O cabo fica entre a viga e a parede, formando um ângulo de 30,0° acima da horizontal. (a) Desenhe o diagrama do corpo livre da viga. (b) Determine a tensão no cabo. (c) Com que força a viga é empurrada para dentro da parede?
Passo 1
E aii galera, vamos fazer mais uma questão?
Bom... o enunciado nos diz que uma viga uniforme de e massa de está presa por uma dobradiça a uma parede e sustentada por um cabo delgado preso a da extremidade livre da viga como mostra a figura:
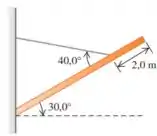
Queremos desenhar o diagrama de corpo livre da viga.
Para isso, devemos analisar todas as forças em todas as direções (inclusive as componentes).
Com isso, poderemos determinar a tensão no cabo e a força que a viga é empurrada para dentro da parede.
Passo 2
Letra a:
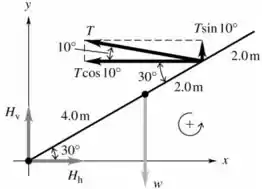
Abaixo, temos o diagrama de corpo livre:
Passo 3
Letra b:
A somatória dos torques é zero, logo:
Assim, pelo diagrama de corpo livre, temos:
Onde é a tensão e é a força peso da viga ().
Assim, isolando , temos:
Passo 4
Letra c:
Sabemos que não há aceleração no sistema. Assim, pela Segunda Lei de Newton, temos que a somatória das forças é igual a zero:
Assim, temos que:
Substituindo , temos:
Resposta
- Ver diagrama