Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.Problemas - Ex. 90
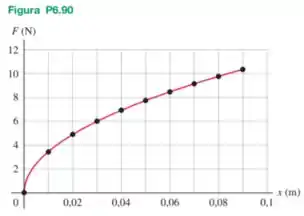
A Figura P6.90 mostra os resultados que a medição da força exerceu sobre as duas extremidades de uma tira elástica para esticá-la a uma distância de sua posição em repouso. Os pontos de dados estão ajustados à equação , onde está em newtons e , em metros. (a) Essa tira elástica obedece à lei de Hooke pela distância mostrada no gráfico? Explique. (b) A rigidez de uma mola que obedece à lei de Hooke é medida pelo valor de sua constante de força , onde . Isso pode ser escrito como para enfatizar as quantidades que estão variando. Defina e calcule como uma função de para essa tira elástica. Para uma mola que obedece à lei de Hooke, é constante, independente de . A rigidez dessa tira, medida por kef, aumenta ou diminui à medida que aumenta, dentro da extensão dos dados? (c) Qual é o trabalho que deverá ser realizado para esticar a tira elástica de até ? E de para ? (d) Uma extremidade da tira elástica está presa a uma haste vertical fixa, e a tira é esticada horizontalmente por a partir de seu comprimento original, não esticado. Um objeto de em uma superfície horizontal e sem atrito é preso à extremidade livre da tira e liberado a partir do repouso. Qual é a velocidade do objeto depois que tiver percorrido ?
Passo 1
Fala galerinha, beleza?
Para resolver esse problema vamos usar a expressão dada no enunciado para a força elástica:
É fácil perceber que essa expressão não é do tipo , de modo que essa tira elástica não obedece à lei de Hooke. Para que a tira obedecesse à lei de Hooke, o gráfico deveria ser uma reta.
No item (b) queremos calcular a derivada da força:
Aí é só usar a regra do tombo:
Portanto,
Conforme aumenta, o denominador aumenta, de modo que diminui. Isso pode ser percebido do gráfico: a inclinação da curva diminui conforme aumenta, indicando que diminui nessa situação!
Passo 2
No item (c), queremos o trabalho entre duas posições distintas. Para isso, fazemos
Na primeira situação, temos
Portanto,
Já na segunda situação, temos que
Logo,
Passo 3
Para resolver o item (c), basta usar o teorema trabalho-energia usando :
Portanto,
Fazendo as contas, achamos