Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 22.Exercícios e Problemas - Ex. 7
Uma fita metálica de largura conduz uma corrente . Portanto, a densidade superficial de corrente é . Calcule a intensidade do campo magnético em pontos próximos à superfície da fita.
Passo 1
Eai pessoal, beleza?
Esse é o primeiro exercício do capítulo em que vamos usar a lei de Ampere! Temos que considerar uma fita metálica conduzindo corrente. A seguir faço um desenho da situação:
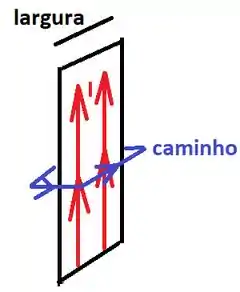
A corrente superficial flui pela fita de baixo para cima. Para achar o campo, consideramos um caminho retangular bem próximo da fita.
As dimensões dessa retângulo são por , onde . Com isso, a integral de linha do campo magnético será
Vamos desprezar em comparação com , de modo que
Passo 2
Agora você chama a lei de Ampere:
Nessa expressão, é a corrente que “fura” o circuito fechado:
Portanto,
Usando a definição do enunciado , achamos
E com isso terminamos esse problema 😉.