Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 22.Exercícios e Problemas - Ex. 4
Um anel de raio igual a , de material supercondutor, conduz uma corrente de . Calcule o campo magnético (a) no centro do anel; (b) em um ponto sobre o eixo do anel, acima do seu centro.
Passo 1
Fala pessoal, beleza?
Para resolver esse problema você deve conhecer a fórmula do campo produzido por um anel de corrente (espira circular) ao longo do seu eixo de simetria:
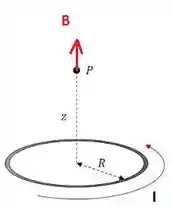
Esse campo é dado por
Aí você precisa perceber que na situação do item (a) temos , já que queremos o campo no centro do anel. Com isso, a fórmula se simplifica para
Agora é só substituir os valores:
Portanto,
Passo 2
Já no item (b), temos a situação em que , de modo que
Fazendo as contas, achamos
Nesse exercício nós basicamente substituímos valores em uma fórmula pronta. Se você quiser olhar em detalhe a dedução dessa fórmula usando a lei de Biot-Savart, aconselho dar uma olhadinha nos resumos do RespondeAí ou na seção 22.4 do livro, mas especificamente na obtenção da equação 22.19.