Numa máquina térmica, o agente é um gás ideal de coeficiente adiabático , que executa o ciclo da figura, onde é uma adiabática e uma isoterma. (a) Calcule o rendimento em função de e . (b) Exprima o resultado em função da razão entre as temperaturas externas. (c) Para e , qual é a razão entre o rendimento obtido e o rendimento de um ciclo de Carnot que opere entre e ?
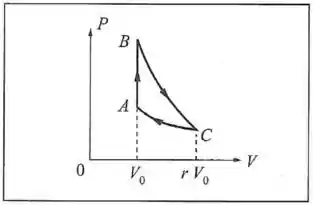
Passo 1
(a) Vamos começar lembrando da fórmula para a eficiência de um motor:
Nosso primeiro passo será calcular o trabalho realizado ao longo do ciclo.
Começando pelo processo adiabático , já que o trajeto é isovolumétrico, e portanto o trabalho é nulo.
O trabalho é um processo adiabático é dado pela seguinte fórmula:
E sabemos que , então vamos fazer .
E vamos calcular a relação entre as pressões, usando a seguinte relação válida para processos adiabáticos:
Então vamos substituir isso na fórmula acima:
Passo 2
Agora vamos olhar para o trecho , que é isotérmico:
Pela lei dos gases ideais :
E podemos comparar os pontos e para melhorar essa expressão:
E podemos calcular a relação entre as temperaturas comparando os pontos e (já que ):
Já calculamos no primeiro passo, e o gráfico deu :
E agora podemos substituir isso na fórmula anterior:
E agora podemos colocar isso na fórmula para :
E então o trabalho total realizado ao longo do ciclo é:
Passo 3
E falta calcular o calor fornecido para o gás.
O processo é adiabático, então , e no trajeto o gás está rejeitando calor. Então só precisamos olhar para o processo :
Agora só precisamos lembrar da relação e :
E então a eficiência é:
Pela lei dos gases ideais temos :
Podemos “trocar” o sinal do primeiro termo do numerador colocando em evidência:
Dividindo a fração por no numerador e denominador:
Passo 4
(b) Agora vamos expressar esse resultado em termos de . Onde e são as temperaturas externas:
Usando a relação que escrevemos antes par as temperaturas e :
Agora vamos reescrever a expressão para :
E podemos fazer a seguinte substituição:
Então:
Passo 5
(c) Para e , o rendimento do ciclo é:
E para o ciclo de Carnot, o rendimento é:
Mas nós calculamos que , então:
Então:
E a razão entre as duas eficiências é:
Resposta
(a) .
(b)
(c) A razão entre os rendimentos é .