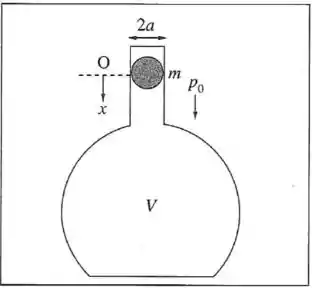
No método de Rüchhardt para medir do ar, usa-se um grande frasco com um gargalo cilíndrico estreito de raio , aberto para a atmosfera ( pressão atmosférica), no qual se ajusta uma bolinha metálica de raio e massa . Na posição de equilíbrio da bolinha, o volume de ar abaixo dela no frasco é . (a) Calcule a força restauradora sobre a bolinha quando ela é empurrada de uma distância ara baixo a partir do equilíbrio, o movimento sendo suficientemente rápido para que o processo seja adiabático. Mostre que a bolinha executa um movimento harmônico simples e calcule o período em função de , , , e . (b) Numa experiência em que , , , , o período observado é . Determine o valor correspondente de para o ar.

Aqui vamos fazer uma aproximação, que deve ser segura quando é pequena o suficiente:

Então, substituindo na equação de cima:

E agora vamos usar a seguinte aproximação:

Onde e :

Beleza, agora sabemos como a pressão varia.

Vamos escrever isso com a segunda lei de Newton:

E como :

Para colocar essa expressão na forma geral do oscilador harmônico, só precisamos reorganizar um pouco:

E do lado direito da equação ficamos com uma constante com a qual não precisamos nos preocupar, já que não interfere na nossa frequência :

E como :

Onde :

(b) Agora vamos usar os valores que foram dados no enunciado para encontrar . Primeiro vamos isola-lo na fórmula que acabamos de demonstrar.

Primeiro elevamos os dois lados ao quadrado:

E depois é só reorganizar:

E substituir com a fórmula para :

E colocando os valores numéricos, lembrando de converter para , e :