Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 31

O fluxo através de um anel é dado por ϕ m = 0,10 t 2 - 0,40 t , onde ϕ m está em webers e t em segundos.

a Esboce gráficos do fluxo magnético e da fem induzida como função do tempo.

b Em que instante(s) o fluxo é mínimo? Qual é a fem induzida neste(s) instante(s)?

c Em que instante(s) o fluxo é zero? Qual é(são) a(s) fem(s) induzida(s) neste(s) instante(s)?

Passo 1

E aí bonit@s, como vocês estão?

Se liguem só, na questão anterior obtivemos a expressão para a fem induzida, dada por

ε t = - 0,20 t - 0,4   V

Assim, para termos o gráfico é só plotar em algum software matemático de modo que vamos obter

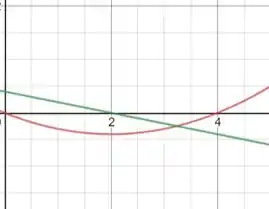
Passo 2

Com o gráfico em mãos percebemos que o fluxo é mínimo em t = 2,0   s e, assim, nossa tensão induzida será ε 2,0 s = 0 .

Passo 3

Novamente observando o gráfico percebemos que o fluxo é igual a 0 para dois pontos: t = 0   e   t = 4,0 s e a fem induzida para esses instantes é igual a - 0,4   V . Voilà tá resolvido mais um exercício, sem muitos problemas.

Resposta

a  

b t = 2,0   s ,     ε 2,0 s = 0

c     t = 0 s   e   t = 4,0 s ,     ε = - 0,4 V   p a r a   a m b o s   o s   c a s o s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura 28-45, considere que a intensidade do campo magnético seja 0,800 T, que a rapidez do bastão seja 10 m/s, que o comprimento dele seja de 20 cm e que a resistência do resistor seja de 2,0Ω . (
No equador, uma bobina de 1000 voltas com seção transversal de 300 cm² e resistência de 15,0 Ω está alinhada de tal forma que seu plano é perpendicular ao campo magnético da Terra, de 0,700 G. (a) Se
Na Figura 28-47, o bastão tem massa m e resistência R . Os trilhos são horizontais, sem atrito e têm resistências desprezíveis. A distância entre os trilhos é l . Uma bateria ideal, com fem ε , está c
Um integrador de corrente mede a corrente como função do tempo e integral (soma) a corrente para determinar a carga total que passa por ele. (Como I = d q / d t , o integrador calcula a integral da co
Um campo magnético uniforme de 1,2T está na direção + z . Um bastão condutor de 15c m de comprimento é paralelo ao eixo y e oscila na direção x com deslocamento dado por x = 2,0c m cos ⁡ 120 π t onde