Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 121

Uma força conservativa F ( x ) age sobre uma partícula de 2,0   k g que se move ao longo de um eixo x . A energia potencial U ( x ) associada a F ( x ) está plotada na Fig. 8-61. Quando a partícula se encontra em x   =   2,0   m , a velocidade é - 1,5   m / s . Quais são (a) o módulo e (b) o sentido de F ( x ) nesta posição? Entre que posições (c) à esquerda e (d) à direita a partícula se move? (e) Qual é a velocidade da partícula em   x   =   7,0   m ?

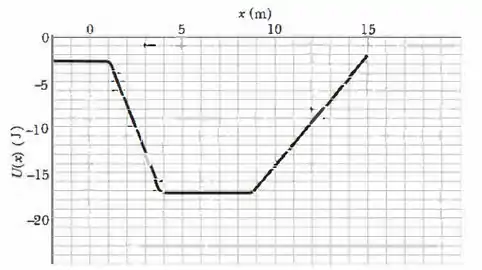
Figura 8-61 Problema 77.

Passo 1

  1. Oi, galerinha! Tudo bom? Para resolver esse problema temos que lembrar que a função que relaciona a energia potencial ( U ( x ) ) e a força conservativa ( F ( x ) ) é dada por

F x = - d U d x

Usando U 1 = - 2,7   J   e   U 4 =   - 17,4   J

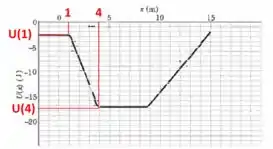
Podemos achar a força,

F = - d U d x ≈ ∆ U ∆ x = - - 17,4 - - 2,7 4 - 1

F = 14,7 3 = 4,9 N

Passo 2

b) Como a derivada de U ( x ) em x = 2   m é negativa, a força é no sentido positivo x

Passo 3

c) De x = 1   m até x = 2   m

∆ U = - W

U 2 - U 1 = - F d

U 2 = U 1 - F d = - 2,7 - 4,9.1

U 2 = - 7,6   J

Logo a energia mecânica total

E = K + U

E = 1 2 m v 2 + U

E = 1 2 2 1,5 2 + - 7,7

E ≈ - 5,5   J

No gráfico existem 2 pontos com este valor x ≈ 1,5   m e x ≈ 13,5   m . Logo, o limite da esquerda é

x ≈ 1,5   m

Passo 4

d) O limite da direita é x ≈ 13,5   m .

Resposta

a) F = 4,9   N

b) sentido positivo x

c) x ≈ 1,5   m

d) x ≈ 13,5   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verdadeiro ou falso: (a) Apenas forças conservativas podem realizar trabalho. (b) Se apenas forgas conservativas atuam sobre uma partícula, a energia cinética da partícula não pode variar. (c) O traba
Verdadeiro ou falso: (a) Apenas forças conservativas podem realizar trabalho. (b) Se apenas forgas conservativas atuam sobre uma partícula, a energia cinética da partícula não pode variar. (c) O traba
Verdadeiro ou falso: (a) Apenas forças conservativas podem realizar trabalho. (b) Se apenas forgas conservativas atuam sobre uma partícula, a energia cinética da partícula não pode variar. (c) O traba
Um bloco de 2,0 kg é empurrado contra uma mola de massa desprezível e constante k=400 N/m, comprimindo a mola até uma distância igual a 0,220 m. Quando o bloco é libertado, ele se move ao longo de uma
Sobre uma superfície horizontal, uma caixa com massa de 50,0 kg é colocada contra uma mola que armazena 360 J de energia. A mola é libertada, e a caixa desliza por 5,60 m antes de parar. Qual é a velo