Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 78

Uma força horizontal constante faz um baú de 50   k g subir 6,0 m em um plano inclinado de 30 ° com velocidade constante. O coeficiente de atrito cinético entre o baú e o plano inclinado é 0,20 . Qual é (a) o trabalho realizado pela força e (b) o aumento da energia térmica do baú e do plano inclinado?

Passo 1

Então galera , a primeira coisa que devemos fazer é construir o diagrama de corpo livre do baú. Aplicando a Segunda Lei de Newton às componentes x e y   das forças envolvidas, obtemos o seguinte sistema de equações:

F 1 cos ⁡ θ - f k - m g sen ⁡ θ = m a

F N - F 1 sen ⁡ θ - m g cos ⁡ θ = 0

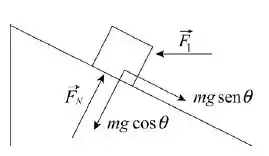
Como o baú está se movendo com velocidade constante ,sabemos que a aceleração é nula. Agora nós podemos substituir f k   por   μ k   F N no sistema de equações acima e achamos que :

F 1 = m g sen ⁡ θ + μ k cos ⁡ θ cos ⁡ θ - μ k sen ⁡ θ

O trabalho realizado pela força F → 1 quando o baú sobe uma distância d ao longo do plano inclinado , por sua vez , é dado por :

W 1 = F 1 d cos ⁡ θ = m g d cos ⁡ θ sen ⁡ θ + μ k cos ⁡ θ cos ⁡ θ - μ k sen ⁡ θ

W 1 = 50 k g 9,8 m s 2 6 m cos ⁡ 30 ° sen ⁡ 30 ° + 0,2 cos ⁡ 30 ° cos ⁡ 30 ° - 0,2 sen ⁡ 30 ° = 2,2 * 10 3 J

Até aqui de boa galera? Bora continuar então!!!

Passo 2

Bom pessoal , nós sabemos que o aumento da energia potencial gravitacional do baú é dado por :

∆ U = m g d sen ⁡ θ = 50 k g 9,8 m s 2 6 m sen ⁡ 30 °   = 1,5 * 10 3 J

Como a velocidade do baú é constante, nós temos que :

W 1 = ∆ U + ∆ E t

Dessa forma , usando números mais precisos que os mostrados acima, o aumento da energia térmica é dado por :

∆ E t = 2,24 *   10 3   J   –   1,47 *   10 3   J   =   7,7 *   10 2   J

Resposta

W 1 = 2,2 * 10 3 J

∆ E t = 7,7 * 10 2 J

Tranquilo galera?? Bora resolver mais questões então!!!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 8 - 52, um bloco desliza ao longo de uma pista, de um nível para outro mais elevado, passando por um vale intermediário. A pista não possui atrito até o bloco atingir o nível mais alto, onde u
Na Fig. 8-51, um bloco de massa m=2,5k g desliza de encontro a uma mola de constante elástica k=320N / m . O bloco para após comprimir a mola 7,5c m . O coeficiente de atrito cinético entre o bloco e
Um pote de biscoitos está subindo um plano inclinado de 40 ° . Em um ponto a 55c m de distância da base do plano inclinado (medidos ao longo do plano), o pote possui uma velocidade de 1,4m / s . O coe
Na Fig. 8-53, um bloco desliza em uma pista sem atrito até chegar a um trecho de comprimento L=0 ,75m , que começa a uma altura h=2,0m em uma rampa de ângulo θ=30 ° . Nesse trecho, o coeficiente de at
A temperatura de um cubo de plástico é medida enquanto o cubo é empurrado 3,0m em um piso, com velocidade constante, por uma força horizontal de 15N . As medidas revelam que a energia térmica do cubo