Um pote de biscoitos está subindo um plano inclinado de . Em um ponto a de distância da base do plano inclinado (medidos ao longo do plano), o pote possui uma velocidade de . O coeficiente de atrito cinético entre o pote e o plano inclinado é . (a) Que distância o pacote ainda sobe ao longo do plano? (b) Qual a velocidade do bloco ao chegar novamente à base do plano inclinado? (c) As respostas dos itens (a) e (b) aumentam, diminuem ou permanecem as mesmas quando o coeficiente de atrito cinético é reduzido (sem alterar a velocidade e a posição do pote)?
Passo 1
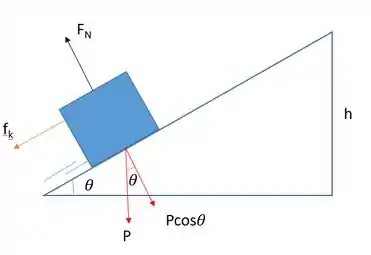
a) Tomando o instante em que o bloco está distante da base como referencial para a energia potencial gravitacional, temos, aplicando a lei de conservação da energia
- No primeiro instante, onde o bloco está distante da base do plano
- No instante em que o bloco para, distante ( da base
Com
E a energia dissipada é dada por
Substituindo os valores encontrados
Para , , e
Passo 2
b) Aplicando a lei da conservação da energia para o ponto onde o bloco para e o instante em que ele chega na base e tomando a base do plano como referencial para a energia potencial gravitacional, teremos
Substituindo os valores, temos
Passo 3
c) Analisando a fórmula usada no item a)
Temos que quanto menor o atrito, maior será o caminho percorrido, pois são inversamente proporcionais. E a velocidade também aumenta quando diminuímos o atrito, pois pela equação do item b)
Percebemos que quanto menor o valor de , menor será o valor subtraído de , o que aumenta a velocidade. Dessa forma, tanto a velocidade quanto a distância aumentam com o atrito cinético reduzido.
Resposta
a)
b)
c) Ambos aumentam