Na Fig. 8-53, um bloco desliza em uma pista sem atrito até chegar a um trecho de comprimento , que começa a uma altura em uma rampa de ângulo . Nesse trecho, o coeficiente de atrito cinético é . O bloco passa pelo ponto com uma velocidade de. Se o bloco pode chegar ao ponto (onde o atrito acaba), qual é sua velocidade neste ponto e, se não pode, qual é a maior altura que atinge acima de ?
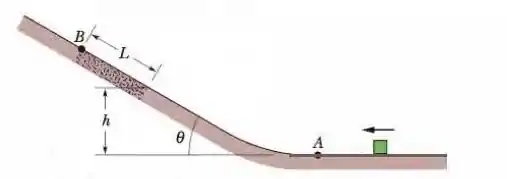
Figura 8-53 Problema 62.
Passo 1
Chamemos o início do terreno acidentado de ponto . A velocidade nesse ponto pode ser encontrada através da Equação de Torricelli entre o ponto e .
Para , e
Passo 2
A energia cinética no ponto pode ser então calculada
Passo 3
A força de atrito no trecho acidentado é
Onde
E a energia dissipada pelo atrito é
Passo 4
A altura do início do trecho acidentado até o seu fim é de
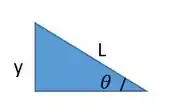
Passo 5
Supondo que o bloco não chega ao ponto , percorrendo então apenas uma distância , teremos
Nesse ponto, toda a energia cinética é transformada em energia térmica e energia potencial. Então
Para , e
Passo 6
Como , a suposição de que o bloco não chega ao ponto está errada. Logo, aplicando a lei de conservação de energia nos pontos e
Para
Resposta
O bloco chega ao ponto e sua velocidade é de .