Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.8 - Ex. 35
A força a que uma partícula está submetida aponta ao longo de um eixo e é dada por ). Determine o trabalho realizado pela força ao mover a partícula de a de duas formas: (a) plotando e medindo o trabalho no gráfico; (b) integrando .
Passo 1
- Oi, pessoal! Tudo bom? O problema nos deu uma equação do primeiro grau relacionando a força aplicada pela distancia,
- Então galera , nós sabemos que dada uma força unidimensional o trabalho executado é a área sob a curva de , ou seja , utilizando a definição , temos que :
)
Como trata-se de uma equação do primeiro grau, nosso gráfico será uma reta. Então para esboça-lo, vamos encontrar o ponto onde a nossa será zero e o ponto onde nosso será zero.
Para
Para
Plotando esses dois pontos no gráfico e traçando a reta, ficamos com,
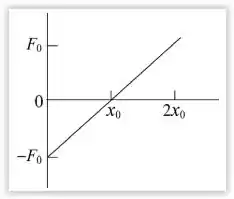
Nesse caso, o trabalho é negativo quando a partícula se desloca de até e positivo quando a partícula se desloca de a , uma vez que a área no 1° caso está abaixo do eixo e no 2° caso a área está acima do eixo .
Para medir a o pelo gráfico, podemos calcular a área da curva. Como a área de um triângulo é dada por , o trabalho realizado de a é :
e o trabalho realizado de até é
O trabalho total é a soma dos dois trabalhos:
Passo 2
Sendo assim :
Reparem que o valor encontrado nos 2 métodos é o mesmo!