Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 60
60. Uma partícula de massa m parte de com . Ao se mover para a direita sobre o eixo , a partícula experimenta uma força variável dada por , onde e são constantes.
a. Qual é a unidade de ?
b. Qual é a unidade de ?
c. Em que posição a força atinge um valor máximo pela primeira vez? Sua resposta deve ser expressa em função das constantes e e talvez de outras constantes numéricas.
d. Esboce o gráfico de em função de desde até .
e. Qual é a velocidade da partícula ao chegar a ? Expresse sua resposta em função de , , e .
Passo 1
Opa! Aqui vamos nós de novo!
a) Olha só! A unidade de força de é o . está multiplicado por .
Qual unidade nos retorna?
Ora bolas! é adimensional! Irá nos retornar nada mais nada menos do que uma constante. Ou seja, a unidade de também é o ...
Passo 2
b) Bora lá pra esse segundo item, agora!
Companheiros e companheiras! O produto é um ângulo, afinal de contas estamos tomando o seno dele.
Sabemos também que um ângulo não possui unidades físicas reais.
Se tiver unidades de , o que a gente espera que aconteça e o produto estiver sem unidade, então deve ter uma unidade, né não?
Bem! Essa unidade vai ser... Igualemos a um, que é um número qualquer, só pra servir de referência.
Como tem unidade de ...
Passo 3
c) Essa letra é moleza!
Repara só!? A força não varia, né!?
Correto! é constante! Mas existe uma coisa que varia... O seno de um ângulo varia segundo a relação abaixo...
Desse modo, o valor máximo para a situação do nosso problema vai acontecer quando for igual a , já que é o valor máximo para qualquer seno.
Mais especificamente, isso vai se dar mesmo se a seguinte condição abaixo for satisfeita;
Como queremo o , então isolemos a variável de posição...
Passo 4
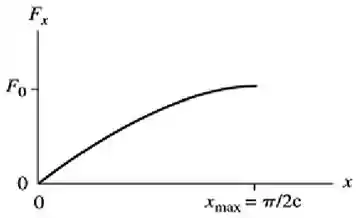
d) E sabendo que nosso gráfico obviamente é senoidal....
E também que existem dois pontos que podemos aproveitar pra fazer o nosso gráfico... Que são:
Chegamos até a seguinte imagem abaixo...
Passo 5
e) Já no caso da velocidade da bolinha em ... Para se resolver este item, vamos começar usando a relação que considera o trabalho igual a variação de energia cinética do sistema...
Como a velocidade inicial é ...
Isolando a velocidade final ...
Obtemos uma boa relação, hein!?
Pra ficar melhor ainda, vamos usar a outra relação abaixo, no qual o trabalho é dado como o produto da força pelo diferencial de posição...
Bom! A partícula sai da posição inicial para a posição qualquer. Sendo assim, nosso limite de integração vai de até ...
Substituindo na expressão pra que descobrimos anteriormente...
Finalmente obtemos nossa resposta!
Resposta
a)
b)
c)
d)
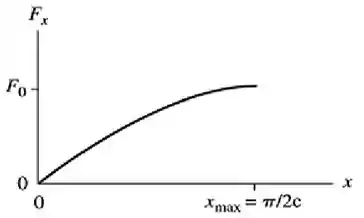
e)