Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 3.3 - Ex. 17
Um jogador de beisebol bate uma bola de forma que ela abandona o bastão com velocidade de , formando um ângulo de acima da horizontal. Despreze a resistência do ar. (a) Ache os dois instantes para os quais a altura da bola está a acima do nível inicial. (b) Calcule os componentes vertical e horizontal da velocidade da bola em cada um dos dois tempos calculados no item (a). (c) Determine o módulo, a direção e o sentido da velocidade da bola quando ela retorna ao nível inicial.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar (a) os dois instantes para os quais a altura da bola está a acima do nível inicial, (b) os componentes vertical e horizontal da velocidade e (c) o módulo, a direção e o sentido da velocidade da bola quando ela retorna ao nível inicial.
Nós sabemos que o jogador bate a bola de forma que ela abandona o bastão com velocidade de , formando um ângulo de acima da horizontal. Então, vamos considerar que a bola de beisebol se move em movimento de projétil com os componentes da velocidade no ponto de lançamento para calcular sua velocidade resultante.
Sendo assim, usando as coordenadas onde a direção é para cima, a direção está para a direita e a origem está no ponto onde a bola de beisebol deixa o bastão, temos as componentes e da velocidade inicial:
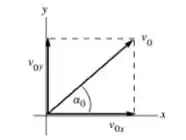
Além disso, vamos considerar que a aceleração horizontal é zero, , e que a aceleração na direção vertical é dada por .
Vamos lá!
Passo 2
Letra a:
Inicialmente, nós sabemos que bola deve estar a acima do nível inicial (), que a velocidade inicial no eixo vertical é , que a aceleração nesse mesmo eixo é a aceleração da gravidade e queremos descobrir o tempo .
Então, vamos usar a equação horária da posição no MRUV, dada por:
Assim, substituindo os dados, vamos ter:
Então, resolvendo essa equação do segundo grau, chegamos em:
Assim, a bola está a uma altura de m acima do ponto onde deixou o taco em . No momento anterior a bola passa por uma altura de conforme seu caminho para cima e, posteriormente, ela passa em sua descida.
Passo 3
Letra b:
Agora vamos calcular os componentes vertical e horizontal da velocidade da bola em cada um dos dois tempos calculados no item (a). Pra isso, vamos considerar a velocidade inicial na direção horizontal:
E a aceleração na direção horizontal:
E usar a equação horária da velocidade na forma:
Assim, com os dados fornecidos, para , temos:
é positivo, ou seja, a bola está viajando para cima.
Para , vamos ter:
é negativo, ou seja, a bola está viajando para baixo.
Passo 4
Letra c:
Agora vamos determinar o módulo, a direção e o sentido da velocidade da bola quando ela retorna ao nível inicial. Pra isso, vamos considerar:
Como, , vamos ter:
Agora usando as componentes calculadas, vamos verificar a magnitude e a direção de :
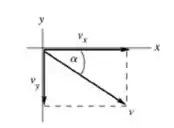
Assim, vamos ter:
E a direção será dada por:
Logo,
abaixo da horizontal.
Isso significa que a velocidade da bola quando ela retorna ao nível em que deixou o taco tem magnitude de e é direcionada em um ângulo de abaixo da horizontal.
Valeu, galera! Até a próxima! 😉
Resposta
- A bola está a uma altura de 10,0 acima do ponto onde deixou o taco em
- A velocidade da bola quando ela retorna ao nível em que deixou o taco tem magnitude de 30,0 m/s e é direcionado em um ângulo de 36,9º abaixo da horizontal.