Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 6.Problemas - Ex. 5

Um garoto que atirar um pedregulho de massa igual a 50g num passarinho pousado num galho 5m a sua frente e 2m acima do seu braço. Para isso utiliza um estilingue em que cada elástico se estica de 1cm para uma força aplicada de 1N. O garoto aponta numa direção a 30 ° da horizontal. De que distância deve puxar os elásticos para acertar o passarinho?

Passo 1

Começaremos calculando a velocidade com que o pedregulho deve sair para acertar o passarinho. Só relembrando nossa fórmula lá da cinemática

y = x t g θ - g 2 ( x 2 v 2 cos 2 ⁡ θ )

→

2 = 5 t g 30 ° - 4,9 .   25 v 2 cos 2 ⁡ 30 °

→

122,5 3 v 2 4 = 5 3 3 - 2

→

4 3 122,5 5 3 3 - 2 = v 2

Substituindo os valores dados obtemos

v 2 = 184,19     m 2 / s 2

Passo 2

Vamos aprender com o Bart agora

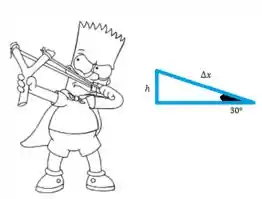
Quando o elástico for esticado e deformado em Δ x o pedregulho vai ficar a uma distância h abaixo da linha de tiro e, portanto, antes que saia com velocidade v a força gravitacional irá realizar um trabalho negativo sobre ele.

W r e s = Δ K

→

W e l + W g = Δ K

→

k Δ x 2 2 - m g h = m v 2 2         ( 1 )

Antes de resolver, vamos calcular   k   e   h .

k = F Δ x

= 1 N e w t o n 1   c m

= 100   N e w t o n s 1   m e t r o

Como são 2 elásticos em paralelo no estilingue, k e q = k 1 + k 2 = 2 k = 200   N / m

h = Δ x s e n 30 ° = Δ x 2

Substituindo em 1 ,

200 Δ x 2 2 - 50   .   10 - 3 9,8   . Δ x 2 = 50   .   10 - 3 . 184,19 2

Reorganizando no formato de equação de segundo grau,

100 Δ x 2 - 0,245 Δ x - 4,6 = 0

a = 100

b = - 0,245

c = - 4,6

Δ x = - b ± b 2 - 4 a c 2 a

= 0,216   c m

Resposta

0,21 6   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 7-9a, um bloco de massa m repousa em uma superfície horizontal sem atrito e está preso a uma mola horizontal (de constante elástica k ) cuja outra extremidade é mantida fixa. O bloco está em r
A única força que age sobre um corpo de 2,0k g enquanto se move no semieixo positivo de um eixo x tem uma componenteF x=- 6 x N , comxemmetros. A velocidade do corpo em x=3,0m é 8 , 0m / s . (a) Qual
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d
Um disco de hóquei tem uma velocidade inicial no sentido +x sobre uma superfície horizontal de gelo. Esboce qualitativamente o gráfico força versus posição para a força horizontal (constante) necessár