Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 6.Problemas - Ex. 14

Um pêndulo é afastado da vertical de um ângulo de 60 ° e solto em repouso. Para que ângulo com a vertical sua velocidade será metade da velocidade máxima atingida pelo pêndulo?

Passo 1

Lembrando da conservação de energia, a velocidade será máxima quando o pêndulo atingir o menor potencial gravitacional, ok? Por isso isso irá ocorrer no ponto mais baixo da trajetória.

K m á x = m g h

→

v m á x 2 = 2 g h

Se nossa velocidade for metade da máxima teremos v = v m á x 2       →

v 2 = v m á x 2 4

= g h 2

Podemos calcular nossa energia cinética por m v 2 2 , então nesse ponto desejado ela será igual a

m g h 4

Para descobrir a energia potencial temos

U = E - K

Neste ponto em que a velocidade é metade da máxima

U = m g h - m g h 4

= m g 3 4 h

Pronto, nossa altura será 3 4   da altura inicial.

Passo 2

Vamos visualizar a situação

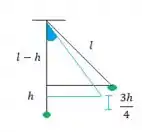
Iniciamente nossa razão é essa

l - h l = c o s 60 °

→

l - h l = 1 2

→

2 l - 2 h = l

Isolando a razão h l

h l = 1 2

Na segunda situação nosso triângulo é o azul e temos

c o s θ = l - 3 h 4 l  

= 1 - 3 4   h l

Juntando nossas equações temos

1 - 3 4 1 2 = c o s θ

→

c o s θ = 5 8

→

θ = a r c o s 5 8 = 51,3 °

Resposta

θ = 51,3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A corda da Fig. 8-36, de comprimento L = 120c m , possui uma bola presa em uma das extremidades e está fixa na outra extremidade. A distância d da extremidade fixa a um pino no ponto P é 75,0c m . A b
Um pêndulo é formado por uma pedra de 2,0k g oscilando na extremidade de uma corda de 4,0m de comprimento e massa desprezível. A pedra tem uma velocidade de 8,0m / s ao passar pelo ponto mais baixo da
A Fig. 8-32 mostra um pêndulo de comprimento L = 1,25m . O peso do pêndulo (no qual está concentrada, para efeitos práticos, toda a massa) tem velocidade v 0 quando a corda faz um ângulo θ 0 = 40,0 °
Um pêndulo consiste em uma pequena bola de massa m presa a um fio de comprimento L . A bola é segurada lateralmente com o fio na horizontal (Figura 7-56). Então ela é largada do repouso. No ponto mais
Um professor de colégio sugeriu, certa vez, o seguinte método para medir a magnitude da aceleração de queda livre: pendure uma massa em um fio bem fino (comprimento L ) para fazer um pêndulo com a mas