Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.2 - Ex. 34
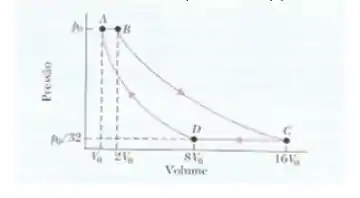
Um gás ideal () é a substância de trabalho de uma máquina térmica que descreve o ciclo mostrado na figura abaixo. Os processos e são reversíveis e adiabáticos. o gás é monoatômico, diatômico ou poliatômico? Qual é a eficiência da máquina?
Passo 1
(a) Faala ae, beleza?
Bom, para determinar se o gás é mono, di ou poliatômico, podemos escolher qualquer processo adiabático. Vou escolher o , beleza?
Sabemos que em uma transformação adiabática temos:
Pelo gráfico temos as seguintes quantidades:
- ;
- ; .
Substituindo na relação acima temos:
Cortando dos dois lados ficamos com:
Colocando na base temos:
Dessa forma, podemos dizer que:
O que equivale a um gás monoatômico.
Passo 2
(b) A eficiência é dada pela expressão:
Nos processos e não há troca de calor, pois são adiabáticos. Então devemos encontrar os calores envolvidos nos processos e .
Passo 3
No processo : calor específico à pressão constante vai ser dado por:
E sabemos que . Como o gás é monoatômico, :
Da lei dos gases ideais temos para o estado :
Para o estado temos:
Assim o calor específico à pressão constante é:
Passo 4
Para determinar o calor da fonte fria, referente ao processo , é precisa calcular o calor específico à pressão constante novamente, mas agora entre outros estados finais e iniciais:
Da lei dos gases ideais temos para o estado :
Para o estado temos:
Assim o calor específico à pressão constante é:
Passo 5
Agora podemos voltar para o passo e resgatar a expressão para a eficiência, pois já determinamos todas as quantidades necessárias: