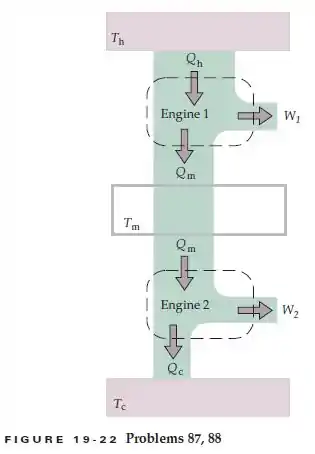
Sejam duas máquinas térmicas conectadas em série, de tal forma que o calor liberado pela primeira máquina seja usado como o calor absorvido pela segunda, como mostrado na Figura 19-22. Suponha que cada máquina seja uma máquina térmica ideal e reversível. A máquina 1 opera entre as temperaturas T qeT m e a máquina 2 opera entre T mef , com T q T mT f . Mostre que o rendimento resultante da combinação é dado por ε c o m b = 1 - T f T q . (Observe que este resultado significa que as duas máquinas térmicas, operando “em série”, são equivalentes a uma máquina térmica reversível operando entre o reservatório mais quente e mais frio).

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 88

Sejam duas máquinas térmicas conectadas em série, de tal forma que o calor liberado pela primeira máquina seja usado como o calor absorvido pela segunda, como mostrado na Figura 19-22. Suponha que cada máquina seja uma máquina térmica ideal e reversível. A máquina 1 opera entre as temperaturas e a máquina 2 opera entre , com . Mostre que o rendimento resultante da combinação é dado por (Observe que este resultado significa que as duas máquinas térmicas, operando “em série”, são equivalentes a uma máquina térmica reversível operando entre o reservatório mais quente e mais frio).

Passo 1

Legal galera, queremos calcular a eficiência da combinação destas duas máquinas. Sabemos que a eficiência é dada pela razão do trabalho total realizado () pelo calor absorvido da temperatura mais alta, que aqui é concordam?

Então como fica esse rendimento?

Agora que calculamos a eficiência da combinação, vamos calcular cada uma separadamente. Começando por 1:

E para 2:

Podemos isolar o trabalho para inserir o resultado na combinação:

Então:

Vamos guardar esta informação!

Passo 2

Vamos expressar agora cada eficiência em função dos calores de entrada e saída. Se lembram?

Por enquanto só essa já nos dá uma informação legal né!? Olhe só se isolarmos a razão:

Agora ficou legal. Vamos colocar na eficiência da combinação e ver o que conseguimos?

Passo 3

Mas não queremos isso, não é? Queremos a eficiência em função das temperaturas.

Então vamos calcular o rendimento para cada máquina em função das suas temperaturas de funcionamento:

Substituindo na combinação:

Então:

Concluindo que:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura abaixo mostra um ciclo reversível a que é submetido 1 m o l de um gás monoatômico ideal. O volume V c = 8 V b . O processo b c é uma expansão adiabática, com p b = 10a t m e V b = 1.10 - 3 m

Um gás ideal ( 1 m o l ) é a substância de trabalho de uma máquina térmica que descreve o ciclo mostrado na figura abaixo. Os processos B C e D A são reversíveis e adiabáticos. ( a ) o gás é monoatômi

O ciclo da figura abaixo representa a operação de um motor de combustão interna a gasolina. O volume V 3 = 4 V 1 . Suponha que a mistura de admissão gasolina-ar é um gás ideal com γ = 1,3 . Qual é a r

Uma máquina térmica, com 20 por cento de rendimento, realiza 0,100 k J de trabalho em cada ciclo. (a) Quanto calor é absorvido do reservatório quente, a cada ciclo? (b) Quanto calor é liberado para o

Uma máquina térmica absorve 0,400 k J de calor e realiza 0,120 k J e trabalho em cada ciclo. (a) Qual é o rendimento da máquina? (b) Quanto calor é liberado para o reservatório frio, a cada ciclo?