Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 10.Problemas - Ex. 58

Você está projetando um sistema elevador simples para um antigo depósito, que está sendo convertido para apartamentos do tipo loft. Um elevador de 22.500 N deverá ser acelerado para cima conectando-o a um contrapeso por meio de um cabo leve (porém forte!), passando por uma polia sólida e uniforme, em forma de disco. O cabo não desliza no ponto de contato com a superfície da polia. Não existe qualquer atrito significativo no eixo da polia, mas sua massa é de 875 kg e ela tem 1,50 m de diâmetro. (a) Qual massa deverá ser a massa do contrapeso de modo que acelere o elevador para cima por 6,75 m nos primeiros 3,00 s, partindo do repouso? (b) Qual é a tensão no cabo em cada lado da polia?

Passo 1

E aiiiiiiiii galera, tudo bom com vocês?

Vamos fazer mais uma questão!!

A segunda lei de Newton em sua forma linear se aplica ao elevador e contrapeso, e em sua forma rotacional se aplica à polia.

Para a polia:

I = 1 2 M R 2

Para o elevador:

m 1 = 22,500 N 9.80 m s 2 = 2300 k g

Abaixo, temos os diagramas de corpo livre para cada pedaço do problema:

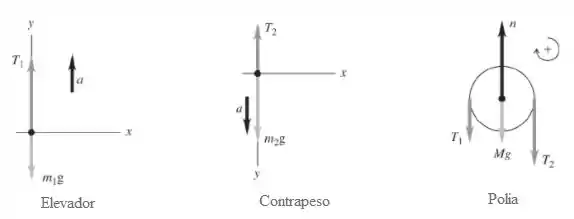
Passo 2

Vamos resolver a letra a e b juntas:

Calcule a aceleração do elevador:

y - y 0 = v 0 y t + 1 2 a y t 2

Que nos dá:

a = 2 y - y 0 t 2 = 2 6.75 m ( 3.00 s ) 2 = 1.50 m s 2

Σ F y = m a y para o elevador nos dá T 1 - m 1 g = m 1 a   e :

T 1 = m 1 a + g = 2300 k g 1.50 m s 2 + 9.80 m s 2 = 2.60 × 10 4 N

Passo 3

∑ τ = I α para o elevador nos dá T 2 - T 1 = 1 2 M R 2 α .

Com α = a R , isso se torna   T 2 - T 1 = 1 2 M a :

T 2 = T 1 + 1 2 M a = 2.60 × 10 4 N + 1 2 875 k g 1.50 m s 2 = 2.67 × 10 4 N

∑ F y = m a y para o contrapeso nos dá m 2 g - T 2 = m 2 a e:

m 2 = T 2 g - a = 2.67 × 10 4 N 9.80 m s 2 - 1.50 m s 2 = 3.22 × 10 3 k g

E w = 3.16 × 10 4 N .

Resposta

Ver resolução

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um aeromodelo com massa 0,750k g é preso ao chão por um fio de modo que voa em um círculo horizontal de raio 30,0m . O motor do avião proporciona um impulso resultante de 0,800N perpendicular ao fio d
A combinação de uma força aplicada e da força de atrito produz um torque total constante de 36,0N⋅m sobre uma roda girando em relação a um eixo fixo. A força aplicada atua por 6,00s . Durante este tem
Um corpo com massa m=5,10k g é preso à extremidade livre de uma corda leve enrolada ao redor de uma bobina de raio R=0,250m e massa M=3,00k g . A bobina é um disco sólido, livre para girar em um plano
Uma batedeira consiste em três barras finas, cada uma com 10,0c m de comprimento. As barras divergem de um ponto central, separadas entre si por 120 ° , e todas giram no mesmo plano. Uma esfera está p
Quando um ginasta trabalhando com argolas executa a cruz de ferro, mantém sua posição em repouso, mostrada na Figura P10.85a. Nesta manobra, os pés do ginasta (não mostrados) não tocam o chão. Os músc