Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 74
Hélio, um gás monatômico, tem inicialmente uma pressão de 16 atm, um volume de 1,0 L e uma temperatura de 600 K. Ele sofre uma expansão quase estática à temperatura constante, até que seu volume seja 4,0 L e, então, é comprimido quase estaticamente, à pressão constante, até que seu volume e temperatura sejam tais que uma compressão adiabática quase estática o reconduz ao seu estado original.
- Esboce este ciclo em um diagrama PV.
- Determine o volume e a temperatura depois da compressão à pressão constante.
- Determine o trabalho realizado durante cada etapa do ciclo.
- Determine o rendimento do ciclo.
Passo 1
Muito bem, queremos o diagrama PV, então precisamos da pressão e do volume para cada ponto.
Vamos começar pelo primeiro processo, expansão isotérmica. Para um gás ideal usamos a fórmula:
Se a temperatura não varia, o termo nRT é constante para o ponto 1 e 2, então:
Já sabemos que:
Então:
O próximo processo é compressão à pressão constante. Então:
Precisamos de , mas se usarmos esse processo será bem mais complicado. Então vamos analisar o próximo, compressão adiabática até seu estado original.
Se temos um processo adiabático podemos usar a relação:
Onde:
Onde g são os graus de liberdade. Para um gás monoatômico,
Isolando e removendo o expoente:
Substituindo:
Agora sim, temos todas as informações para o diagrama!
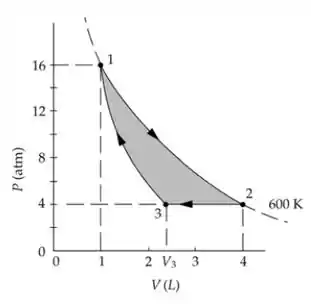
Passo 2
Na letra b queremos o volume e a temperatura depois da compressão à pressão constante, ou seja, e . Já resolvemos o volume enquanto fazíamos o diagrama, não é? Então vamos para a temperatura.
Vou optar pelo caminho de 1 até 3, compressão adiabática. Para esse caso, temos uma relação que vai nos ajudar bastante:
Isolando a temperatura:
Substituindo:
Passo 3
Muito bem, para a letra c nós precisamos calcular o trabalho para cada etapa do ciclo.
No primeiro processo, isotérmico, o trabalho é calculado como:
Não temos o número de mols, mas sabemos da relação para os gases ideais:
Substituindo no trabalho:
Lançando os dados:
No segundo processo, à pressão constante, podemos calcular o trabalho por:
Substituindo os dados:
Para finalizar, o processo adiabático. E o trabalho é dado por:
Lembrando que:
E sabendo que
Substituindo:
É trabalhoso, mas não difícil !
Passo 4
Estamos acabando, só precisamos da eficiência do ciclo. E como calcular?
O trabalho total será a soma de todos os trabalhos encontrados no passo 3:
O único processo onde temos o calor sendo absorvido é processo de
Como este processo é isotérmico, não há variação da energia interna. Então:
Substituindo:
Em porcentagem: