Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 83

Um ciclo prático comum, frequentemente usado em refrigeração, é o ciclo de Brayton, que envolve (1) uma compressão adiabática, (2) uma expansão isobárica (pressão constante), (3) uma expansão adiabática e (4) uma compressão isobárica de volta ao estado original. Suponha que o sistema comece a compressão adiabática a temperatura T 1 e sofra transições para as temperaturas T 2 , T 3   e   T 4 após cada etapa do ciclo.

  1. Esboce este ciclo em um diagrama PV.
  2. Mostre que o rendimento do ciclo completo é dada por ε = 1 - T 4 - T 1 T 3 - T 2 .
  3. Mostre que este rendimento pode ser escrito como ε = 1 - r 1 - γ γ , onde r é a razão de pressão P a l t a P b a i x a (a razão entre as pressões máximas e mínimas no ciclo).

Passo 1

Bom, queremos o diagrama do ciclo de Brayton. Que é composto de:

  1. Compressão adiabática: neste caso não há troca de calor, o volume está diminuindo e aumentando a pressão;
  2. Expansão isobárica: há um aumento do volume mantendo a pressão constante, então estão inserindo calor no ciclo;
  3. Expansão adiabática: não há troca de calor, o volume está aumentando e a pressão diminuindo;
  4. Compressão isobárica de volta ao estado original: há diminuição do volume mantendo a pressão constante, então estão removendo calor no ciclo.

Desenhando o ciclo:

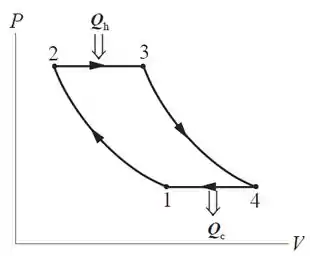
Essa até que foi fácil! Vamos continuar!

Passo 2

A eficiência é calculada como:

ε = 1 - Q c Q q

Como o calor Q c é o calor liberado do processo 14, Q 14 , temos:

Q 14 = - Q c

Como temos um processo à pressão constante, podemos calculá-lo como:

Q 14 = - n C p ∆ T = - n C p ( T 1 - T 4 )

Já o calor Q q é o calor absorvido durante o processo 23, Q 23 , então:

Q q = Q 23

Como temos um processo à pressão constante, podemos calculá-lo como:

Q 23 = n C p ∆ T = n C p ( T 3 - T 2 )

Substituindo na eficiência:

ε = 1 - - n C p ( T 1 - T 4 ) n C p ( T 3 - T 2 )

Reorganizando:

ε = 1 - ( T 4 - T 1 ) ( T 3 - T 2 )

Passo 3

Nós vamos terminar achando o rendimento em função da razão entre as pressões.

Antes de começar nós devemos perceber que vamos precisa da relação entre temperatura e pressão. E temos, não é?

Para processos adiabáticos, como 12 e 34, vale a seguinte relação:

T 1 γ P m e n o r γ - 1 = T 2 γ P m a i o r γ - 1

Isolando T 1 :

T 1 = T 2 P m e n o r P m a i o r γ - 1 γ

Para 34:

T 4 γ P m e n o r γ - 1 = T 3 γ P m a i o r γ - 1

Isolando T 4 :

T 4 = T 3 P m e n o r P m a i o r γ - 1 γ

Substituindo na eficiência do passo 1:

ε = 1 - T 3 P m e n o r P m a i o r γ - 1 γ - T 2 P m e n o r P m a i o r γ - 1 γ T 3 - T 2  

Isolando a razão entre as pressões:

ε = 1 - T 3 - T 2 P m e n o r P m a i o r γ - 1 γ T 3 - T 2 = 1 - P m e n o r P m a i o r γ - 1 γ

Sabendo que:

r = P m a i o r P m e n o r

Então a eficiência será:

ε = 1 - r 1 - γ γ

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Compare o rendimento do ciclo Otto com o rendimento do ciclo de Carnot operando entre as mesmas temperaturas máxima e mínima. (O ciclo Otto é discutido na Seção 19-1).
A figura abaixo mostra uma máquina de Carnot que trabalha entre as temperaturas T 1 = 400 K e T 2 = 150 K e alimenta um reservatório de Carnot que trabalha entre as temperaturas T 3 = 325 K e T 4 = 22
Uma máquina de Carnot opera com uma potência de 500W entre fontes de 100 ° C e 60,0 ° C . Calcule (a) a taxa de entrada de calor e (b) a taxa de saída de calor.
A figura mostra um ciclo de Carnot em um diagrama T - S . A escala do eixo horizontal é definida por S S = 0,60J / K . Determine (a) a transferência líquida de calor por ciclo e (b) o trabalho líquido
Uma máquina de Carnot opera entre dois reservatórios com temperaturas de 520K e 300K . a) Se a máquina recebe 6,45k J de calor do reservatório a 520K em cada ciclo, quantos joules por ciclo ela rejeit