Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.2 - Ex. 10
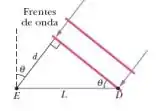
(Ilusão causada pela água). Uma das informações usadas pelo cérebro humano para determinar a localização de uma fonte sonora é a diferença entre o instante em que um som é detectado pelo ouvido mais próximo da fonte e o instante em que é detectado pelo outro ouvido. Suponha que a fonte está suficientemente distante para que as frentes de onda sejam praticamente planas e seja a distância entre os ouvidos. (a) Se a direção da fonte faz um perpendicular ao plano do rosto (Fig. 17-30), qual é o valor de em termos de D e da velocidade do som no ar? ( b) Se um pessoa está debaixo d'água e a fonte está exatamente à direita, qual é o valor de em termos de e da velocidade do som na água? (c)Com base na diferença , o cérebro calcula erroneamente que a direção da fonte faz um ângulo com uma perpendicular ao plano do rosto. Determine o valor de para água doce a .
Passo 1
Show de bola pessoal, primeiro de tudo é a gente perceber que o atraso é devido à distância que cada frente de onda tem que percorrer até atingir a orelha esquerda, localizada em , após alcançar a direita, em Daí, da figura do enunciado, a gente consegue relacionar essas constantes e encontrar assim:
Logo:
Tal que é a velocidade do som.
Passo 2
(b)Usamos o mesmo raciocínio anterior, mas com a ressalva de que a velocidade do som na água, é diferente da velocidade do som no ar, representado por . Nesse caso, como a fonte está exatamente à direita, Assim, temos:
Passo 3
(c)Aqui, a gente vai precisar usar um dado fornecido na Tabela 17-1 do livro. Nela, podemos ver que a velocidade do som na água doce a ( é igual a .Assim, com base na diferença , temos:
E então: