Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.3 - Ex. 41
Como indicado na Figura , o bloco (massa de ) está em repouso sobre o topo de uma mesa. Ele é ligado a um bloco (massa de ) por uma corda horizontal que passa sobre uma polia leve e sem atrito. O coeficiente de atrito cinético entre o bloco A e o topo da mesa é de . Depois que os blocos são libertados, ache a) a velocidade de cada bloco depois de terem se movido 3,0 cm; b) a tensão na corda. Inclua um diagrama do corpo livre ou os diagramas que você usou para achar suas respostas.
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
O enunciado nos deu um sistema com dois blocos ligados por um cabo que passa por uma polia e que são liberados pela ação da gravidade, especificamente pelo pelo do bloco .
Vamos analisar a situação descrita no enunciado e esboçar o sistema:
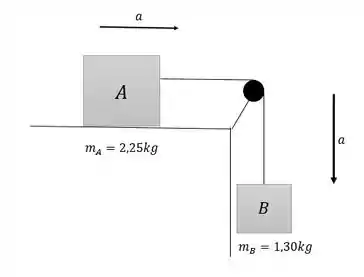
Para cada bloco, vamos adotar como positivo a direção coordenada para ser a direção da aceleração do bloco.
Como os dois blocos estão presos por uma única corda, a aceleração é a mesma para ambos.
As variáveis que queremos encontrar são a tensão,, no cordão e as aceleração, , de um dos blocos. Então pode ser usada em uma equação de aceleração constante para encontrar a velocidade de cada bloco. Vamos lá!
Passo 2
Para o bloco que está em cima da mesa, vamos esboçar um diagrama de corpo livre:
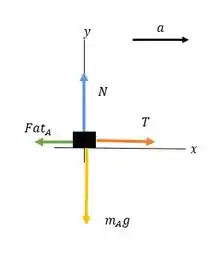
E aplicar a 2º Lei de Newton nesse bloco, .
Primeiro, na direção de :
Então, somando as forças verticais no bloco:
Temos a força normal de superfície :
Como a força de atrito cinética é dada por:
Substituindo , vamos ter:
Agora, calculando as forças na direção de :
Temos:
Substituindo , ficamos com:
Passo 3
Para o bloco que está suspenso, vamos esboçar seu diagrama de corpo livre:
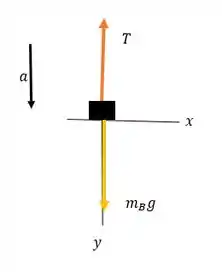
E aplicar a 2º Lei de Newton nesse bloco, :
Nesse caso, só temos forças na direção :
E isolando a tensão , ficamos com:
Passo 4
a) O que temos que fazer agora é pegar essa ultima equação, onde encontramos :
E substitui-la em:
Assim, ficamos com:
Colocando as massas em evidência:
E isolando :
Substituindo os valores do enunciado, temos:
Passo 5
Então, para encontrar a velocidade final, como não temos o tempo, vamos precisar da equação de Torricelli:
Onde é a aceleração horizontal calculada no passo anterior, é o deslocamento considerado e é a velocidade inicial.
Os blocos estão ligados por uma mesma corda, então sabemos que eles têm as mesmas velocidades.
Isolando a velocidade na equação de Torricelli e usando os dados do enunciado, temos:
Passo 6
Então, vamos calcular a tensão, , na corda, pela relação que encontramos ali em cima:
Colocando em evidência:
Então, temos que:
A força exercida pelo cordão tem o mesmo valor para cada bloco. Além disso, se o bloco suspenso acelera para baixo.
Também, . Então, e o bloco na mesa acelera na direção da tensão .
Valeu, galera! Até a próxima! 😉