Exercícios de Atrito Estático + Atrito Cinético - Lista de Exercícios Resolvida
Questão 1
Dois blocos e , um sobre o outro, deslocam-se rampa abaixo com uma força aplicada sobre o bloco . Os blocos movem-se conjuntamente a velocidade constante de . O coeficiente de atrito cinético entre o bloco e a rampa é , e o coeficiente de atrito estático entre os blocos é . A rampa faz com a superfície horizontal. O bloco da figura pesa e o bloco pesa .
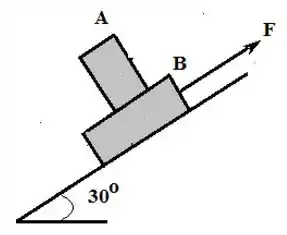
Desenhe dois diagramas do corpo livre separados mostrando as forças que atuam sobre e sobre .
Determine a força necessária para que os blocos apresentem o movimento descrito.
Quais são as intensidades e o sentido da força de atrito no bloco ?
Ver solução completaQuestão 2
A figura a seguir mostra o bloco () conectado a uma parede rígida por uma corda ideal, repousando sobre o bloco (). O bloco está submetido a uma força horizontal para a direita que pode variar em módulo. Adote .
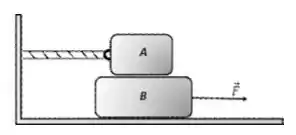
O sistema repousa sobre um solo que oferece atrito desprezível. Só existe atrito na superfície entre os blocos (). A situação inicial é de repouso.
a) Faça o diagrama de corpo livre para cada um dos blocos isoladamente. Não calcule valores, apenas nomeie todas as forças que agem em cada bloco.
b) Para o caso em que , e supondo que a corda não se rompe, calcule os vetores força de todas as outras forças que agem sobre os blocos. Use o sistema de coordenadas padrão: eixo positivo apontando para a direita, eixo positivo apontando para cima. (Dica: calcule primeiro o valor da fora de atrito estático máximo entre os blocos.)
c) Para o caso em que , calcule os módulos da aceleração do bloco e da força de tração da corda sobre o bloco , supondo que a corda não se rompe.
d) Suponha agora que a corda não exista, mas que todos os outros dados do enunciado principal sejam repetidos. Calcule o valor máximo que a força pode assumir de tal modo que não haja deslizamento relativo entre os blocos, ou seja, eles aceleram juntos.
Ver solução completaQuestão 3
Na figura abaixo, as massas dos blocos 2 e 3 são e , respectivamente. O coeficiente de atrito cinético entre o bloco 2 e a mesa é 0,10 enquanto o coeficiente de atrito estático é 0,20. Despreze o atrito entre os blocos 1 e 2.
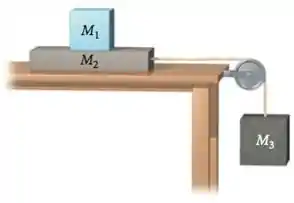
a) Usando a 3a Lei de Newton, faça o diagrama do corpo livre para cada um dos três blocos, indicando todos os pares de ação e reação.
b) Qual deve ser o valor mínimo da massa do bloco 1 para que o bloco 2 não se mova?
c) Calcule a aceleração do sistema se o bloco 1 é levantado.
d) Esboce os gráficos da velocidade e da posição do bloco 2, desde o momento em que o bloco 1 é levantado até após este momento.
Ver solução completaQuestão 4
Seja a situação apresentada na figura abaixo, consistindo de dois blocos de massas (bloco menor) e (bloco maior). Uma força horizontal de módulo é aplicada ao bloco menor. O coeficiente de atrito estático entre os blocos é 0,40 e o de atrito cinético é 0,35. O coeficiente de atrito estático entre o bloco e o solo é 0,30 e o coeficiente de atrito cinético é 0,25.
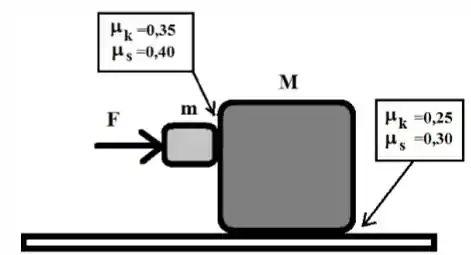
a) Nesta situação, o conjunto dos dois blocos se movimenta na horizontal? Justifique sua resposta através de cálculos explícitos.
b) Calcule a força de atrito entre os dois blocos, argumentando, com cálculos, se esta força é estática ou cinética.
Ver solução completaQuestão 5
Um corpo de massa escorrega sobre um plano horizontal com coeficiente de atrito cinético e estático , como na figura. Um conjunto de polia e corda sem massa e sem atrito liga este corpo a outro corpo de massa , pendurado na vertical.
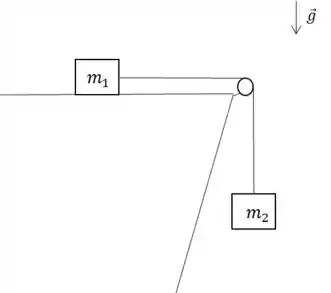
a) Calcule a aceleração do sistema.
b) Calcule a nova aceleração do sistema se colocamos um corpo de massa firmemente preso sobre o corpo 1.
c) Para a situação do item , qual deveria ser a massa mínima de modo que e se movessem em qualquer situação?
Ver solução completaQuestão 6
Um bloco de massa está sob a ação de uma força horizontal constante sobre uma superficie horizontal sem atrito. Sobre ele há um bloco de massa , preso à esquerda por um fio ideal. Este fio passa por uma roldana ideal que encontra-se fixa a uma parede vertical, e o conecta ao bloco de massa . Os segmentos do fio são paralelos ao plano horizontal; vide a figura abaixo. Suponha que haja atrito entre os blocos em contato entre si. Considere como conhecidos os valores dos coeficientes de atrito estático e cinético , as massas e e o módulo da aceleração da gravidade .
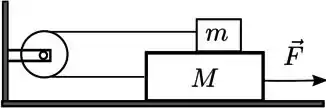
- Isole os blocos e represente por meio de um diagrama de corpo livre todas as forças que atuam em cada um deles.
- Suponha inicialmente que os blocos estejam em repouso. Determine o valor máximo do módulo de , para que o sistema permaneça em repouso.
- Considere agora que , cujo módulo é igual a , seja capaz de colocar os blocos em movimento com aceleração constante. Para o intervalo de tempo no qual os blocos permanecem em contanto entre si, determine os vetores aceleração de cada bloco em função de , , , e .
- Determine o módulo da tração do fio, para o caso do item anterior c)
Questão 7
Um corpo de massa escorrega sobre um plano horizontal com coeficiente de atrito cinético e estático , como na figura. Um conjunto de polia e corda sem massa e sem atrito liga este corpo a outro corpo de massa , pendurado na vertical.
a) Calcule a aceleração do sistema.
b) Calcule a nova aceleração do sistema se colocamos um corpo de massa firmemente preso sobre o corpo 1.
c) Para a situação do item , qual deveria ser a massa mínima de modo que e se movessem em qualquer situação?
Ver solução completaQuestão 8
A figura a seguir mostra o bloco () conectado a uma parede rígida por uma corda ideal, repousando sobre o bloco (). O bloco está submetido a uma força horizontal para a direita que pode variar em módulo. Adote .
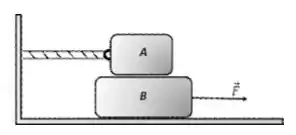
O sistema repousa sobre um solo que oferece atrito desprezível. Só existe atrito na superfície entre os blocos (). A situação inicial é de repouso.
a) Faça o diagrama de corpo livre para cada um dos blocos isoladamente. Não calcule valores, apenas nomeie todas as forças que agem em cada bloco.
b) Para o caso em que , e supondo que a corda não se rompe, calcule os vetores força de todas as outras forças que agem sobre os blocos. Use o sistema de coordenadas padrão: eixo positivo apontando para a direita, eixo positivo apontando para cima. (Dica: calcule primeiro o valor da fora de atrito estático máximo entre os blocos.)
c) Para o caso em que , calcule os módulos da aceleração do bloco e da força de tração da corda sobre o bloco , supondo que a corda não se rompe.
d) Suponha agora que a corda não exista, mas que todos os outros dados do enunciado principal sejam repetidos. Calcule o valor máximo que a força pode assumir de tal modo que não haja deslizamento relativo entre os blocos, ou seja, eles aceleram juntos.
Ver solução completaQuestão 9
Dois blocos escorregam juntos sobre uma superfície horizontal sem atrito. O bloco de cima tem massa e de baixo e o atrito entre elas tem um coeficiente estático . Uma força horizontal de módulo atua sobre o bloco de baixo. Qual é a condição sobre para que os dois blocos não deslizam entre si?
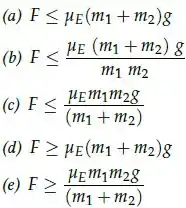
Questão 11
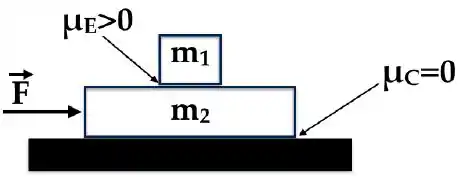
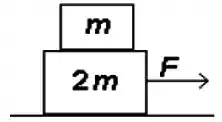
Uma pequena caixa de massa é colocada em cima de uma caixa maior de massa como mostrado na figura. Quando uma força é aplicada na caixa grande, ambas as caixas se movem para a direita com a mesma aceleração. Supondo que o coeficiente de atrito entre todas as superfícies é , qual é a força atuando na massa menor?
a)
b)
c)
d)
e)
Ver solução completaQuestão 12
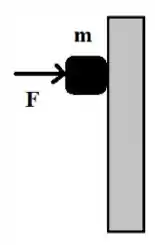
a) Na figura acima, um bloco de massa é empurrado contra uma parede por uma força horizontal de módulo . O coeficiente de atrito estático entre a parede e o bloco é 0,35. Verifique, através de cálculos explícitos, se nestas condições o bloco fica em repouso ou cai deslizando pela parede.
Seja agora a situação apresentada na figura abaixo, consistindo de dois blocos de massas (bloco menor) e (bloco maior). Uma força horizontal de módulo é aplicada ao bloco menor. O coeficiente de atrito estático entre os blocos é 0,40 e o de atrito cinético é 0,35. O coeficiente de atrito estático entre o bloco e o solo é 0,30 e o coeficiente de atrito cinético é 0,25.
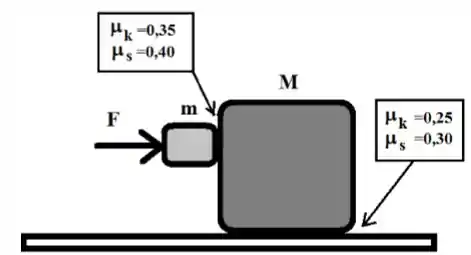
b) Nesta situação, o conjunto dos dois blocos se movimenta na horizontal? Justifique sua resposta através de cálculos explícitos.
c) Calcule a força de atrito entre os dois blocos, argumentando, com cálculos, se esta força é estática ou cinética.
Ver solução completaQuestão 13
Dois blocos e , um sobre o outro, deslocam-se rampa abaixo com uma força aplicada sobre o bloco . Os blocos movem-se conjuntamente a velocidade constante de . O coeficiente de atrito cinético entre o bloco e a rampa é , e o coeficiente de atrito estático entre os blocos é . A rampa faz com a superfície horizontal. O bloco da figura pesa e o bloco pesa .
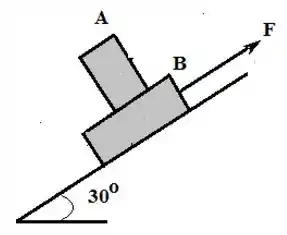
Desenhe dois diagramas do corpo livre separados mostrando as forças que atuam sobre e sobre .
Determine a força necessária para que os blocos apresentem o movimento descrito.
Quais são as intensidades e o sentido da força de atrito no bloco ?
Ver solução completaQuestão 15
Um bloco de massa igual a 10 kg é empurrado continuamente contra uma parede vertical por uma força horizontal de intensidade igual 100 N, como mostrado na primeira figura. O coeficiente de atrito estático entre o bloco e a parede é igual a 0,60 e o coeficiente de atrito cinético é igual a 0,40. O bloco está inicialmente em repouso. Tanto no item (a) quanto no item (b) , faça um diagrama de corpo livre do bloco e use g=10 m/ .
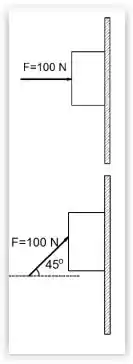
(a) (1,0 ponto) O que acontece com o bloco? Justifique a resposta.
(b) (1,0 ponto) Se a mesma força de 100N for aplicada com inclinação para cima de 45° em relação à horizontal, como mostra a segunda figura, o que acontece com o bloco? Justifique a resposta.
Ver solução completaQuestão 16
(Cap 6 – Ex 65) Um bloco de massa é colocado em cima de um outro bloco de massa . Para fazer o bloco de cima deslizar sobre o bloco de baixo enquanto o segundo é mantido fixo, é preciso aplicar ao bloco de cima uma força horizontal de no mínimo . O conjunto de blocos é colocado sobre uma mesa horizontal sem atrito (Fig. 6-47). Determine o módulo (a) da maior força horizontal que pode ser aplicada ao bloco de baixo sem que os blocos deixem de se mover juntos e (b) a aceleração resultante dos blocos.
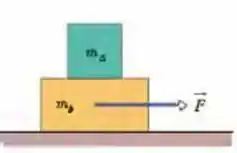
Questão 17
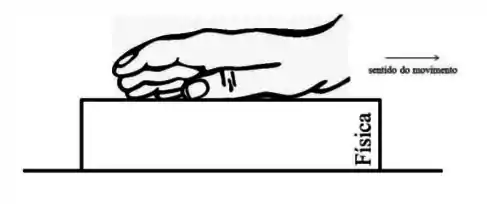
Um livro de Física de massa está em repouso sobre uma mesa. O coeficiente de atrito estático entre a mesa e o livro é de e o coeficiente cinético é . Uma pessoa, para mover o livro, aplica uma força com a mão (massa desprezível) na parte superior do livro, puxando-o em sua direção a um a velocidade constante, como mostra a figura. O coeficiente de atrito estático entre a mão e o livro é de .
(a) Faça um diagrama de corpo livre para a mão e o livro indicando as forças do problema. No caso da mão, indique claramente como deve ser a força aplicada para colocar o sistema em movimento.
(b) Caso a componente vertical aplicada no livro seja de , calcule a força Normal exercida pela mesa no livro e a força de atrito cinético entre estas duas superfícies.
(c) Calcule qual a força horizontal aplicada para que o livro se mova com velocidade constante na situação do item anterior.
(d) Encontre as componentes da força mínima que deve ser aplicada para manter o livro em movimento sem que a mão escorregue.
Questão 18
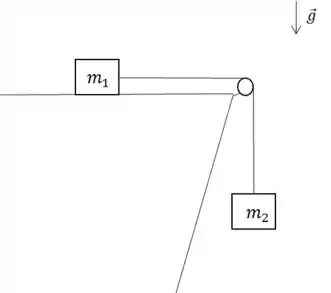
Dois blocos estão ligados por uma corda que passa por uma polia de massa desprezível e sem atrito em seu eixo, como mostra a figura ao lado.
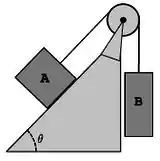
O bloco A tem massa e os coeficientes de atrito estático e cinético entre A e a rampa são respectivamente
e
Considere que os corpos são liberados a partir do repouso, , e .
(a) Determine a menor massa possível do bloco B acima da qual o bloco A sobe a rampa.
(b) Determine a maior massa possível do bloco B abaixo da qual o bloco A desce a rampa.
(c) Obtenha a aceleração do bloco A quando a massa de B é indicando o módulo, direção e sentido.
Ver solução completaQuestão 19
Uma caixa de está em repouso sobre uma superfície horizontal. Os coeficientes de atrito estático e cinético entre o par de superfícies são respectivamente e . Uma força horizontal de é aplicada sobre a caixa. A força de atrito exercida pela superfície sobre a caixa é:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 20
Um bloco de massa m = 2,0 kg encontra-se inicialmente em repouso sobre uma mesa horizontal. Os coeficientes de atrito estático e cinético entre o bloco e a mesa valem μe = 0,40 e μc = 0,20, respectivamente. Uma força F de módulo 20 N é então aplicada ao bloco, fazendo um ângulo θ com a horizontal. Considere .
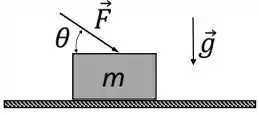
Sabendo que cos θ = 0,80 e sen θ = 0,60, a aceleração do bloco durante a aplicação da força F é:
a) 0
b) 1,6
c) 2,4
d) 4,8
e) 6,0
f) 6,8
g) 8,0
h) 9,6
i) 9,8
Ver solução completaQuestão 21
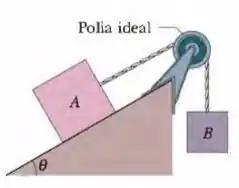
Um bloco de massa encontra-se inicialmente mantido em repouso sobre um plano inclinado de um ângulo , preso a uma das pontas de uma corda ideal (veja a Figura 2). A corda passa por uma polia ideal e tem a sua outra ponta presa a um bloco de massa . Os coeficientes de atrito estático e cinético entre e o plano inclinado são e , respectivamente. Considere , e . Num certo instante, o conjunto dos blocos é liberado.
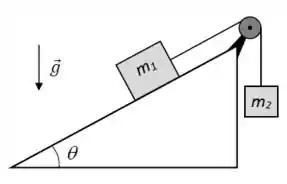
- Faça o diagrama de corpo livre de cada bloco depois que o conjunto é liberado, desenhando e nomeando todas as forças que atuam sobre eles.
- Calcule o módulo da força normal que o plano inclinado exerce sobre .
- Depois de liberado, o conjunto se move? Justifique sua resposta.
- Calcule o módulo da força de tração na corda.
- Calcule o módulo da força de atrito e especifique seu sentido.
Questão 22
Uma caixa está em repouso sobre uma superfície horizontal áspera. Os coeficientes de atrito estático e cinético entre a caixa e a superfície são µe = 0,40 e µc = 0,20, respectivamente.
(a) Para pôr a caixa em movimento horizontal com a menor força aplicada possível, a força aplicada deve ser horizontal, fazer um ângulo abaixo da horizontal ou um ângulo acima da horizontal? Justifique qualitativamente sua resposta.
(b) Se o peso da caixa é 50 N e a força aplicada faz um ângulo de 30° acima da horizontal, determine a intensidade mínima da força aplicada capaz de pôr a caixa em movimento horizontal.
(c) Nas condições do item anterior, supondo que a força externa mínima que dá início ao movimento horizontal é atingida e mantida, a caixa se moverá com velocidade constante ou aceleração constante? Justifique a resposta.
Ver solução completaQuestão 23
Os freios ABS para automóveis foram desenvolvidos de modo que os pneus não deslizassem
nas frenagens. Avalie as alternativas quanto à sua veracidade:
I. Um dos motivos para o desenvolvimento desse freio foi aproveitar o fato que o coeficiente de atrito estático é maior do que o cinético
II. Como o carro está em movimento, usa-se o coeficiente de atrito cinético para calcular a força de atrito entre os pneus e a estrada.
III. Se durante a frenagem o motorista quiser desviar de um obstáculo, é melhor que o pneu esteja escorregando - portanto o freio ABS não ajuda nesse caso.
São corretas as afirmações:
a) somente I
b) somente II
c) somente III
d) I e II
e) todas as afirmações
Ver solução completaQuestão 24
Um bloco de massa é mantido em repouso, pressionado contra uma parede vertical por uma força de módulo , conforme mostra a figura. Sabendo que os coeficientes de atrito estático e cinético entre o bloco e a parede são, respectivamente, e , o que pode-se afirmar sobre o módulo da força de atrito entre a parede e o bloco?
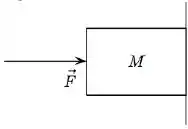
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 25
Um bloco de massa se encontra sobre a superfície de um plano inclinado de ângulo . Um bloco , de massa , colocado em cima do bloco , está unido por um fio ideal a um pino fixo, como mostra a figura.
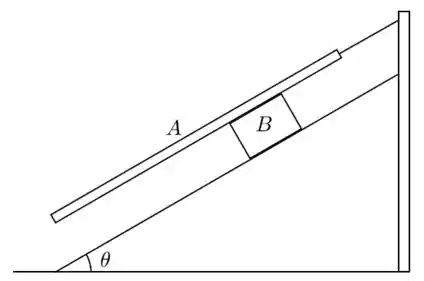
Ao liberar o bloco ele desliza sobre o plano, mantendo contato com o bloco . Se o coeficiente de atrito cinético entre todas as superfícies em contato é :
- Faça o diagrama das forças para cada bloco.
- Calcule a tração no fio.
- Determine a aceleração de descida do bloco .
Expresse os resultados em termos de , , e .
Ver solução completaQuestão 26
[Enunciado comum às Questões 3 e 4]
Uma força atua horizontalmente sobre um bloco de massa e que se encontra apoiado em uma parede vertical, como mostrado na figura. O coeficiente de atrito estático entre o bloco e a parede é . Considere o módulo da aceleração gravitacional no local .
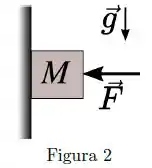
[Questão 3]
Considere as assertivas:
. Se , o bloco desce com aceleração constante.
. Se , o bloco permanece em repouso.
. Se , o bloco permanece em repouso.
Marque a alternativa abaixo contendo apenas as assertivas corretas.
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 27
(Cap 6 – Ex 31 ) Na Fig. 6-34, os blocos e pesam e , respectivamente. (a) Determine o menor peso do bloco que evita que o bloco deslize, se entre e a mesa é . (b) O bloco é removido bruscamente de cima do bloco . Qual é a aceleração do bloco se entre e a mesa é ?
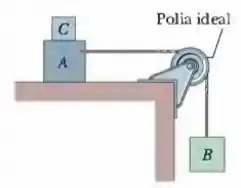
Questão 28
(Cap 6 – Ex 34) Na Fig. 6-37, uma prancha de massa repousa em um piso sem atrito e um bloco de massa repousa sobre a prancha. O coeficiente de atrito estático entre o bloco e a prancha é e o coeficiente de atrito cinético é . O bloco é puxado por uma força horizontal de módulo . Em termos dos vetores unitários, qual é a aceleração (a) do bloco e (b) da prancha?
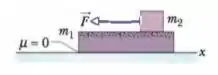
Questão 30
[ENUNCIADO COMUM ÀS QUESTÕES 10 e 11]
Considere o seguinte experimento para medirmos o coeficiente de atrito estático entre duas superfícies. Colocamos um bloco sobre um plano inclinado cuja inclinação podemos controlar. Inicialmente o plano está na horizontal. Lentamente, aumentamos o ângulo entre o plano e a horizontal, como na figura. Sobre essa situação responda as questões 10 e 11.
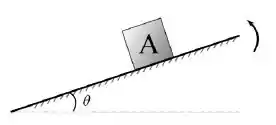
[QUESTÃO 11]
Logo após o bloco começar a descer o plano inclinado, é correto afirmar que:
(A) O bloco desce com velocidade constante.
(B) A força da gravidade sobre o bloco é igual à força de atrito.
(C) O bloco desce de forma desacelerada.
(D) O bloco desce de forma acelerada.
(E) O módulo da força de atrito aumenta à medida que o bloco desce.
Ver solução completaQuestão 31
No esquema mostrado na figura , o carrinho de massa pode deslizar sem atrito, enquanto os coeficientes de atrito entre e a superfície horizontal valem e e .
Qual deve ser o menor valor de para que se inicie o movimento?
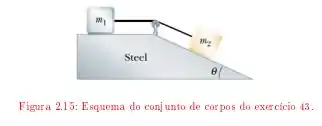
Questão 32
No esquema mostrado na figura , o carrinho de massa pode deslizar sem atrito, enquanto os coeficientes de atrito entre e a superfície horizontal valem e e .
Qual será a tensão na corda se e ?
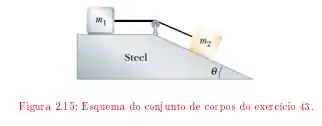
Questão 33
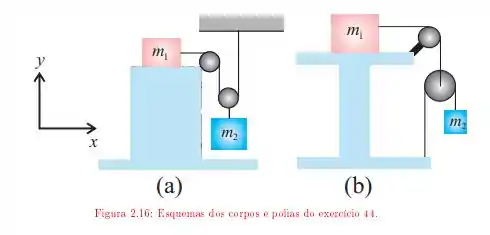
Os esquemas de corpos e polias na figura mostram sistemas constituídos por blocos de massas e e roldanas ideais, uma fixa e a outra móvel, pelas quais passam fios inextensíveis. As massas das roldanas e dos fios são desprezíveis comparadas às dos blocos. O bloco está apoiado em uma mesa e os coeficientes de atrito entre eles valem e . Para cada um dos esquemas, determine:
O valor máximo da relação de modo que o sistema permaneça em equilíbrio;
Questão 34
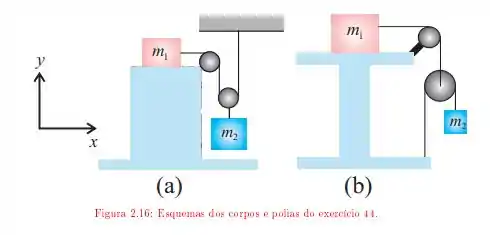
Os esquemas de corpos e polias na figura mostram sistemas constituídos por blocos de massas e e roldanas ideais, uma fixa e a outra móvel, pelas quais passam fios inextensíveis. As massas das roldanas e dos fios são desprezíveis comparadas às dos blocos. O bloco está apoiado em uma mesa e os coeficientes de atrito entre eles valem e . Para cada um dos esquemas, determine:
A aceleração da massa quando:
Figura e ;
Figura e ;
Questão 35
Os esquemas de corpos e polias na figura mostram sistemas constituídos por blocos de massas e e roldanas ideais, uma fixa e a outra móvel, pelas quais passam fios inextensíveis. As massas das roldanas e dos fios são desprezíveis comparadas às dos blocos. O bloco está apoiado em uma mesa e os coeficientes de atrito entre eles valem e . Para cada um dos esquemas, determine:
O vetor força que a haste, que suporta a roldana fixa, exerce sobre a mesa, em termos dos versores cartesianos e .
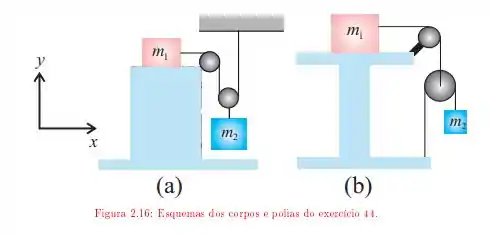
Questão 36
Dois blocos de massas e estão ligados por um fio ideal que passa por uma polia ideal fixa numa parede. Os coeficientes de atrito estático e cinético entre os blocos valem e , respectivamente, e os coeficientes de atrito estático e cinético entre a massa e o solo valem e . Se a aceleração relativa entre os blocos é de , o valor do módulo da força horizontal aplicada a é:
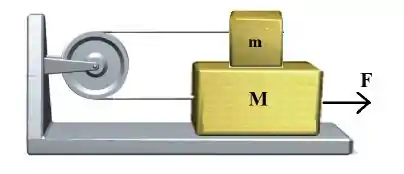
Questão 37
(Cap 6 – Ex 15) O coeficiente de atrito estático entre o Teflon e ovos mexidos é cerca de . Qual é o menor ângulo com a horizontal que faz com que os ovos deslizem no fundo de uma frigideira revestida com Teflon?
Ver solução completaQuestão 38
(Cap 6 – Ex 14) A Fig. 6-20 mostra um bloco inicialmente estacionário de massa sobre um piso. Uma força de módulo é aplicada com um ângulo para cima. Qual é o módulo da aceleração do bloco se (a) e e (b) e ?
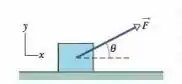
Questão 39
Três blocos massivos são colocadas em um sistema, conforme a figura. As massas dos blocos e valem ambas , e a massa do bloco vale . A inclinação de ambos os planos inclinados é a mesma e vale . As polias e os fios são ideais. Use para a aceleração da gravidade. Dê as respostas em termos dos dados fornecidos pelo enunciado. (Observação, quando os blocos estão se movendo, os módulos de suas respectivas acelerações possuem o mesmo valor)
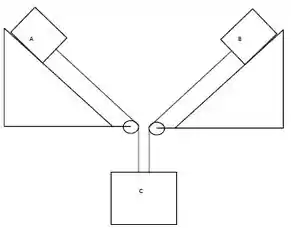
Inicialmente suponha que não há atrito entre os planos e os blocos e .
a) Faça o diagrama de corpo livre para os blocos , e .
b) Determine a aceleração do sistema.
Suponha agora que exista atrito entre os blocos A e B e os planos inclinados, e que os seus valores são idênticos.
c) Faça o diagrama de corpo livre desta nova situação.
d) Calcule o coeficiente de atrito estático mínimo entre os planos e os blocos e para os blocos permanecerem em repouso.
e) Caso os blocos já estejam se movendo, e o coeficiente de atrito cinético seja , calcule a aceleração do sistema.
Ver solução completaQuestão 40
5) Uma força , de módulo 12 N, pressiona um bloco de massa m = 0,5 Kg contra uma parede vertical, como mostra a figura. O coeficiente de atrito estático entre a parede e o bloco é e o cinético é . Utilize, neste problema, para o módulo da aceleração da gravidade. Sobre esta situação, é correto afirmar que
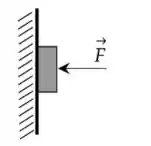
(a) a força total que a parede exerce sobre o bloco tem módulo 13 N e o bloco não escorrega.
(b) a força total que a parede exerce sobre o bloco tem módulo 17 N e o bloco não escorrega.
(c) a força total que a parede exerce sobre o bloco tem módulo 12 N e o bloco não escorrega.
(d) a força total que a parede exerce sobre o bloco tem módulo 5 N e o bloco escorrega.
(e) a força total que a parede exerce sobre o bloco tem módulo 5 N e o bloco não escorrega.
Ver solução completaQuestão 41
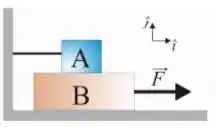
Q - O bloco de peso está preso a uma parede por meio de uma corda. Ele está colocado sobre o bloco que pesa e é puxado por uma força . O coeficiente de atrito nas superfícies inferior e superior do bloco é . O módulo da força necessária para arrastar o bloco com aceleração , mantendo-se o bloco em repouso, em Newtons, é:
Questão 42
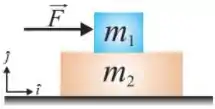
Q - Um bloco de massa é colocado sobre um bloco de massa , que encontra-se em repouso. Admita que os coeficientes de atrito estático e cinético entre os blocos são e , respectivamente, e que os coeficientes de atrito estático e cinético entre o bloco de massa e o solo são e , respectivamente. Netas condições, o máximo valor de , em Newtons, que aplicada ao corpo de massa movimenta o sistema sem que os blocos se desloquem relativamente um ao outro é:
Questão 43
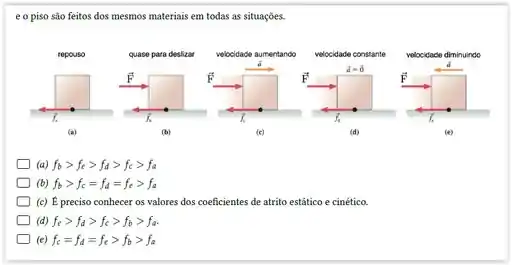
Dois blocos idênticos são puxados ao longo de uma superfície, como na figura. Qual das seguintes afirmações é falsa?
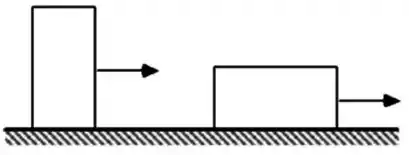
- Uma força de mesmo módulo é necessária para iniciar o movimento dos blocos em ambos os casos;
- O coeficiente de atrito cinético é o mesmo nos dois casos;
- A força normal exercida pela superfície sobre os blocos é a mesma nos dois casos;
- O módulo da força de atrito cinético é maior no bloco da direita;
- Uma força de mesmo módulo é necessária para movimentar os dois blocos com a mesma aceleração;
Questão 45
(Cap 6 – Ex 29) O bloco da Fig. 6-33 pesa e o bloco pesa . Os coeficientes de atrito entre e a rampa são e . O ângulo é igual a . Suponha que o eixo é paralelo à rampa, com o sentido positivo para cima. Em termos dos vetores unitários, qual é a aceleração de se está inicialmente (a) em repouso, (b) subindo a rampa e (c) descendo a rampa?