Duas caixas estão ligadas por uma corda sobre uma superfície horizontal (Figura ). A caixa possui massa e a caixa possui massa . O coeficiente de atrito cinético entre cada caixa e a superfície é . As caixas são empurradas para a direita com velocidade constante por uma força horizontal . Em termos de , de e de , calcule a) o módulo da força ; b) a tensão na corda que conecta os blocos. Inclua um diagrama do corpo livre ou os diagramas que você usou para achar suas respostas.

Vamos desenhar o diagrama de corpo livre da caixa e aplicar a 2º Lei de Newton sobre ele:

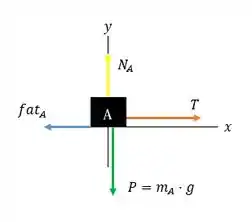
Sabemos que: , então:

Para o eixo :

Somando as forças verticais no bloco , temos:

E isolando a força normal :

Para o eixo , vamos ter:

Somando as forças horizontais no bloco:

Só que , que é a força de atrito cinético, é dada por , onde é a força normal no bloco que encontramos no passo anterior. Então, substituindo, temos:

Agora, vamos desenhar o diagrama de corpo livre da caixa e aplicar a 2º Lei de Newton sobre ele:

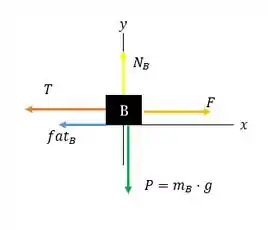
Para o eixo :

Calculando as forças verticais no bloco:

Para o eixo :

Então, substituindo , temos:

E encontramos a força de tração nos blocos.

b) Pronto, encontramos as equações dos dois blocos, então vamos usar:

E substitui-la em na seguinte equação:

Assim, ficamos com:

Podemos organizar um pouquinho, colocando em evidência:

E a tensão na corda será igual a força de atrito do bloco A. Logo:

Valeu, galera! Até a próxima! 😉