Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.3 - Ex. 45
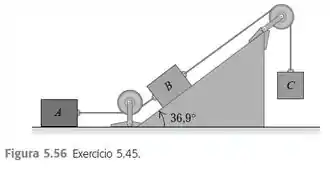
Os blocos A, B e C são dispostos como indicado na Figura 5.56, e ligados por cordas de massas desprezíveis. O peso de A é de 25,0 N e o peso de B também é de 25,0 N. O coeficiente de
atrito cinético entre cada bloco e a superfície é igual . O bloco C desce com velocidade constante. a) Desenhe dois diagramas do corpo livre separados mostrando as forças que atuam sobre A e sobre B. b) Ache a tensão na corda que liga o bloco A ao B. c) Qual é o peso do bloco C? d) Se a corda que liga o bloco A ao B fosse cortada, qual seria a aceleração do bloco C?
Passo 1
Oi, galerinha! Tudo bom?
Nesse problema temos três blocos , e são dispostos como indicado na figura do enunciado e ligados por cordas de massas desprezíveis.
O peso de é de e o peso de também é de . O coeficiente de atrito cinético entre cada bloco e a superfície é igual . O bloco desce com velocidade constante.
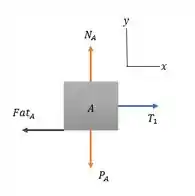
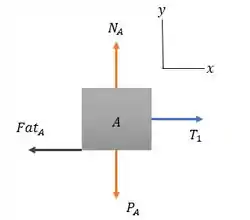
A partir daí temos que desenhar dois diagramas do corpo livre separados mostrando as forças que atuam sobre e sobre .
Além disso temos que achar a tensão na corda que liga o bloco ao , o peso do bloco e se a corda que liga o bloco ao fosse cortada, qual seria a aceleração do bloco .
Tem ideia de como fazemos isso?
Vamos analisar onde vamos colocar as forças e desenhar o diagrama de corpo livre para cada bloco pedido.
Veja só!
Passo 2
Para o bloco A:
- O bloco tem massa, logo tem uma força peso apontado para baixo;
- Como está encostado em uma superfície, tem uma força normal, , agindo sobre ele;
- Existe um fio preso a ele, logo tem uma força de tensão;
- Existe um atrito, e seu coeficiente é: .
Como os três blocos estão ligados e o bloco C está caindo, o bloco A está indo para a direita, ou seja, a força de atrito é contraria a isso, apontando para a esquerda.
Sacou?
Passo 3
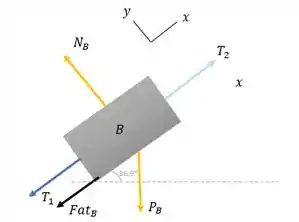
Para o bloco B:
- O bloco tem massa, logo temos uma força peso apontada para baixo;
- O bloco está em contato com uma superfície inclinada, logo a força normal é perpedincular ao plano;
- Existe um fio conectado a ele, havendo uma força de tensão;
- Tem um atrito, o mesmo do bloco A: .
Como os três blocos estão ligados e o bloco C está caindo, faz com que o bloco B está subindo o plano inclinado, ou seja, a força de atrito é contrária a isso, apontando para baixo.
Vale destacar que como o bloco tem velocidade constante e o bloco e estão todos conectados a ele, e também estão em velocidades constantes.
Tranquilo até aqui?
Passo 4
No item b) para achar a tensão na corda que liga o bloco ao , devemos fazer o equilíbrio em cada bloco. Vamos calcular pelo bloco .
No bloco , a única força que atua no é , e como a velocidade é constante, ele está em equilíbrio em todos os movimentos.
Deste modo, no temos:
Substituindo os valores,
Bacana, não é?
Passo 5
No item c) para encontrarmos o peso do bloco C, vamos fazer seu diagrama de corpo livre:
- Ele tem massa;
- Ele não está encostado em nenhuma superfície;
- Existe um fio que o prende;
- Não existe nenhum atrito.
Então:
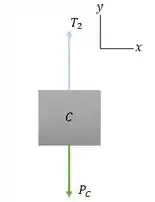
Como ele está com velocidade constante, ele está em equilíbrio em todos os movimentos.
No :
Então, para encontrarmos o peso de C, devemos achar . Para isso, vamos fazer o equilíbrio do bloco B.
Estamos quase lá!
Passo 6
No :
Concorda?
Passo 7
No :
Devemos encontrar a sua componente horizontal usando a “regra do Colado, Separado”
Está acompanhando?
Passo 8
Teremos então:
Substituindo os valores,
Lagal, né?
Passo 9
E no item d) antes que a corda entre A e B seja cortada, a força no sistema é zero. Quando a corda é cortada a força de atrito em A é removida do sistema e há uma força no sistema dos blocos B e C.
Então temos que:
Substituindo os valores,
E aí! entendeu tudo? Responde Aí!
