Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 87

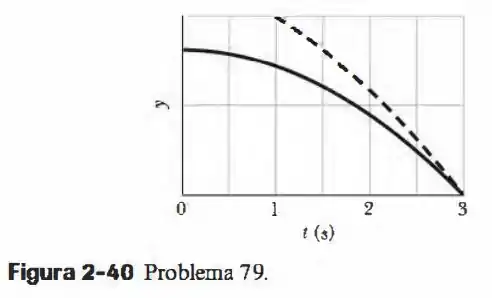
No instante t   =   0 , um alpinista deixa cair um grampo, sem velocidade inicial, do alto de um paredão. Após um curto intervalo de tempo, o companheiro de escalada, que está 10   m acima, lança outro grampo para baixo. A F i g .   2 - 40 mostra as posições y dos grampos durante a queda em função do tempo t . Com que velocidade o segundo grampo foi lançado?

Passo 1

Note que o gráfico nos informa que o segundo grampo é lançado 1 segundo após o primeiro grampo ter caído, então se adotarmos t 2 como o tempo de queda do segundo grampo e t 1 o tempo de queda do segundo grampo então temos que:

t 2 = t 1 - 1

Fazendo t 1 = t , então a equação de posição vertical de cada grampo será em termos de t iguais a:

y = y 0 + v 0 y t + a 2 t 2

y 1 = y - g 2 t 2

y 2 = y + 10 - v 0 y ( t - 1 ) - g 2 t - 1 2

Adotando a altura inicial do primeiro grampo como y então automaticamente a altura inicial do segundo grampo será de y + 10 e fizemos a velocidade inicial do segundo grampo ser para baixo igual a - v 0 y

Passo 2

Como y 1 = y 2 = 0 para t = 3   s (que é o tempo onde ambos tocam o chão nós teremos:

y - g 2 t 2 = y + 10 - v 0 y ( t - 1 ) - g 2 t - 1 2

Isolando v 0 y temos:

v 0 y = 10 + g 2 t 2 - g 2 t - 1 2 t - 1

Como g = 9.81   m / s 2 e t = 3   s

v 0 y = 10 + 9.81 2 ⋅ 3 2 - 9.81 2 3 - 1 2 3 - 1

v 0 y = 17.26   m / s

Resposta

v 0 y = 17.26   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

82. Uma bola de borracha é atirada diretamente para cima, a partir do solo, com rapidez inicial v 0 . Simultaneamente, uma segunda bola de borracha é solta, a partir do repouso, de uma altura h em rel
62. Heather e Jerry estão em pé sobre uma ponte 50m acima de um rio. Heather atira uma pedra diretamente para baixo com velocidade de 20m / s . No mesmo instante, Jerry atira uma pedra diretamente par
63 . Nicole arremessa uma bola diretamente para cima. Chad observa a bola a partir de uma janela 5,0m acima do ponto de onde Nicole a lança. A bola passa por Chad na subida e tem velocidade de 10m / s
Bolas são feitas deixando-se cair gotas esféricas de metal derretido no interior de uma torre alta –chamada de torre de queda –, as quais se solidificam durante a queda. a. Se uma bola precisa de 4,0
Um estudante em pé no solo arremessa uma bola diretamente para cima. A bola sai da mão do estudante com rapidez de 15 m/s quando sua mão se encontra 2,0 m acima do solo. Que distância ela percorrerá n