Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 61

O isótopo do carbono 14 C é usado para realizar datação de artefatos arqueológicos por meio do carbono. O 14 C (massa de 2,34 ×   10 - 26   k g ) decai pelo processo conhecido como decaimento beta, em que o núcleo emite um elétron (a partícula beta) e uma partícula subatômica chamada de neutrino. Em um desses decaimentos, o elétron e o neutrino são emitidos formando um ângulo reto um com o outro. O elétron (massa de 9,11 ×   10 - 31   k g ) possui velocidade de   5,0 ×   10 7   m / s , e o neutrino possui um momentum de 8,0 ×   10 - 24   k g   m / s . Quanto vale a velocidade de recuo do núcleo?

Passo 1

A parte mais difícil desse problema é desenhar a representação desse sistema (e que não é difícil), segue a imagem:

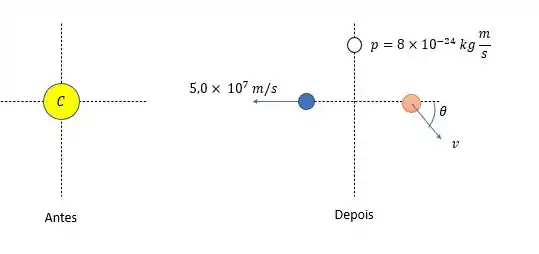
A orientação dos três (neutrino, elétron e núcleo) não importa, somente importa o neutrino estar perpendicular ao elétron.

Fazendo a somatória do momento linear nós temos:

0 = - m e l e t r o n ⋅ v e l e t r o n + p n e u t r i n o j ^ + m n u c l e o v cos ⁡ θ i ^ - s e n θ j ^

Onde a massa do núcleo vale:

m n u c l e o = m c a r b o n o 14 - m e l e t r o n = 2,34 ×   10 - 26 - 9,11 ×   10 - 31 = 2.3399 × 10 - 26

Então:

0 = - 9,11 ×   10 - 31 ⋅ 5 × 10 - 7 i ^ + 8 × 10 - 24 j ^ + 2.3399 × 10 - 26 v cos ⁡ θ i ^ - s e n θ j ^

Passo 2

Igualando as partes com i ^ e com j ^ nós teremos:

0 = - 9,11 ×   10 - 31 ⋅ 5 × 10 7 + 2.3399 × 10 - 26 v c o s   θ

v c o s   θ = 1 946.66

8 × 10 - 24 = 2.3399 × 10 - 26 v s e n   θ

v   s e n   θ = 341.895

Fazendo a soma dos quadrados desses dois valores nós temos:

v s e n   θ 2 + v cos ⁡ θ 2 = 1946.66 2 + 341.895 2

v = 1976   m / s

Resposta

v = 1976   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desabamento de um edifício. Na seção reta de um edifício que aparece na Fig. 9-7la, a infraestrutura de um andar qualquer, K , deve ser capaz de sustentar o peso P de todos os andares que estão acima.
Um carro de 1400k g está se movendo inicialmente para o norte a 5,3m / s , no sentido positivo de um eixo y . Depois de fazer uma curva de 90 ° para a direita em 4,6s , o motorista desatento bate em u
Uma bola de 0,15k g se choca com uma parede com uma velocidade de ( 5,00m / s ) i+( 6,50m / s ) }+( 4,00m / s ) k , ricocheteia naparede e passa a ter uma velocidade de ( 2,00m / s ) i+( 3,50m / s ) ]
Uma bola de140g com uma velocidade escalar de 7,8m / s se choca perpendicularmente com uma parede e ricocheteia no sentido oposto com a mesma velocidade escalar. O choque dura 3,80m s . Quais são os m
Uma metralhadora de chumbinho dispara dez balas de 2,0g por segundo com uma velocidade escalar de 500m / s . As balas são paradas por uma parede rígida. Determine (a) o módulo do momento de cada bala,