Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 45
45. Um equilibrista de está em pé sobre o centro de uma corda esticada horizontalmente. Os suportes da corda se encontram a um do outro e a corda forma com a horizontal nas duas extremidades. O equilibrista se abaixa um pouco e depois salta da corda com aceleração de a fim de apanhar um trapézio que passa por ele. Quanto vale a tensão na corda quando ele salta?
Passo 1
A primeira coisa que precisamos fazer é desenhar o diagrama de forças tanto do equilibrista quando da corda para que possamos analisar todo o sistema.
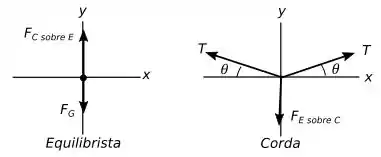
Outra coisa que podemos tirar do enunciado é que nada ele diz sobre a massa da corda, sendo assim podemos considerar como uma corda ideal (sem massa) e com isso podemos tratar a tensão de forma uniforme na corda e acredite, isso facilita bastante pra gente.
Passo 2
Como queremos a tração da corda vamos olhar o diagrama dela e usar a Segunda Lei de Newton com todas as forças aplicadas sobre ela:
é a força que o equilibrista faz sobre a corda
Vimos no Passo 1 que a corda não tem massa, sendo assim:
Substituindo o que temos e rejeitando:
Opa opa, não sabemos que é e precisamos dessa informação para achar , então, como vamos fazer?
Vem comigo que eu mostro.
Passo 3
Podemos ver no diagrama de forças que é par ação/reação de , isso significa que sabemos que o módulo da força é igual (apenas o sentido é diferente), ou seja, vamos usar novamente a Segunda Lei de Newton mas agora no equilibrista para poder descobrir quem é .
Substituindo o que temos:
Como o exercício quer, apenas, quanto vale a tensão e não o sentido em que ela aponta podemos jogar esse mesmo na última equação do passo anterior.
Resposta