Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 77
77. Um jardineiro empurra um cortador de grama de cujo cabo está inclinado acima da horizontal. O coeficiente de atrito de rolamento do cortador de grama é de . Que potência o jardineiro deve desenvolver a fim de empurrar o cortador a uma velocidade constante de ? Considere que ele empurre paralelamente ao cabo.
Passo 1
Bom! A melhor forma de se começar resolvendo esse problema, é realizar um esboço do que está acontecendo em nosso problema.
Ou seja, bora deixar de conversa fiada e fazer o diagrama de corpo livre para o nosso cortador que é onde tá sendo aplicada a força.
Aqui está...
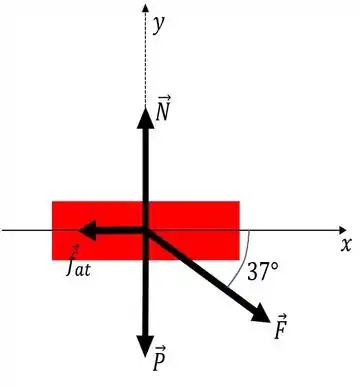
Consideramos o cortador como uma caixa, afinal praticidade é tudo que a gente quer.
Passo 2
Sendo assim, não há muito o que se pensar em fazer, né!?
Só nos resta aplicar o somatório das forças na direção ... Lembrando que o nosso carrinho não tem aceleração nesse direção...
Como a normal multiplicada pelo coeficiente de atrito do cortador de grama nos dá a força de atrito , então...
Logo, ficamos com...
Passo 3
Em seguida, bora aplicar o somatório das forças em .
Uma vez que o objetivo é o cortador ter velocidade constante nessa direção, o somatório das forças tem que ser igual a zero... Sendo assim:
Pegando a expressão para a que descobrimos no e substituindo na igualdade anterior...
Obtemos o valor da força aplicada pelo cortador!
Passo 4
Por fim! Para achar a potência gerada pela força para que o carrinho se mova na direção horizontal, basta multiplicá-la pela velocidade.
Só um “porém” aqui! A potência pedida é pro carro se mover na direção horizontal, já que é nessa direção que o cortador está indo! Sendo assim, precisamos multiplicar a nossa força por no cálculo.
Obtemos então, que...
E pronto! Fechamos o capítulo!
Agradecimento aos envolvidos!
E até a próxima!