Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 74

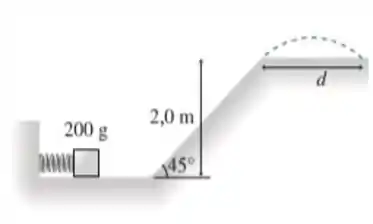
74. A mola da FIGURA PD11.74 possui constante elástica de 1000   N / m . Ela é comprimida em 15   c m e, depois, lança um bloco de 200   g . A superfície horizontal é livre de atrito, porém o coeficiente de atrito cinético do bloco na rampa é de 0,20 . Que distância d , o bloco voa pelo ar?

Passo 1

Opa! Aqui vamos nós de novo!

Olha só! Pra entender melhor esse problema, vamos começar fazendo um esboço mais ou menos do que tá acontecendo até nosso bloquinho ser lançado numa distância d ...

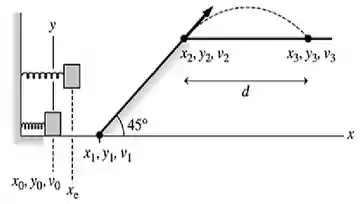
Passo 2

Bom! Temos que descobrir o valor da velocidade do bloco quando ele é lançado. Por isso, vamos aproveitar apenas os instantes ( 0 ) e ( 2 ) .

Sendo assim, o melhor jeito pra se fazer isso é relacionando as energias em 0 e ( 2 ) .

Só que tem um detalhe importante aí! A nossa rampa tem atrito, logo a energia presente em ( 0 ) não é igual a energia presente em ( 2 ) .

Mas ainda podemos relacioná-las, né não!? Você não concorda que a energia em ( 2 ) é igual a energia em ( 0 ) menos o trabalho dissipativo da força de atrito? Hein!?

Pois bem! É isso mesmo!

Fazendo o diagrama de corpo livre para o bloco quando está na rampa, podemos entender melhor...

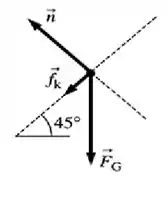
Desse modo, a seguinte relação é valida...

E 0 - W f k = E 2

U 0 + K 0 - W f k = U 2 + K 2

Só pra constar! A única energia presente em ( 0 ) é a energia potencial elástica, dada por...

U 0 = 1 2 k ( x 0 - x e ) 2

O que nos faz ficar, olhando a figura do P a s s o   1 pra tirar as expressões das outras energias; com...

1 2 k ( x 0 - x e ) 2 - f k y 2 sen ⁡ 45 ° = m g y 2 + 1 2 m v 2 2

Como a força de atrito é o produto da normal n → pelo coeficiente de atrito μ k . Sendo que a normal n → vale:

n = m g cos ⁡ 45 °

Então, ficamos com...

1 2 k ( x 0 - x e ) 2 - m g μ k cos ⁡ 45 ° y 2 sen ⁡ 45 ° = m g y 2 + 1 2 m v 2 2

Isolando v 2 ...

1 2 m v 2 2 = 1 2 k ( x 0 - x e ) 2 - m g μ k cos ⁡ 45 ° y 2 sen ⁡ 45 ° - m g y 2

m v 2 2 = k ( x 0 - x e ) 2 - 2 m g μ k cos ⁡ 45 ° y 2 sen ⁡ 45 ° - 2 m g y 2

v 2 2 = k m ( x 0 - x e ) 2 - 2 g μ k cos ⁡ 45 ° y 2 sen ⁡ 45 ° - 2 g y 2

v 2 = k m ( x 0 - x e ) 2 - 2 g μ k cos ⁡ 45 ° y 2 sen ⁡ 45 ° - 2 g y 2

E em seguida, substituindos os valores correspondentes a cada variável...

v 2 = 1000   N / m 0,20   k g ( 0,15   m ) 2 - 2 ( 9,8   m / s ² ) ( 0,20 ) cos ⁡ 45 ° 2,0   m sen ⁡ 45 ° - 2 ( 9,81   m / s ² ) ( 2,0   m )

v 2 = 8,091   m / s

Finalmente obtemos a velocidade com que o bloquinho sai da rampa!

Passo 3

Pelo que podemos ver da figura do P a s s o   1 , o nosso bloco é lançado de ( 2 ) até ( 3 ) executando o que chamamos de movimento oblíquo, que é composto de um movimento uniforme, na direção horizontal, e de um movimento acelerado, na vertical.

No caso do movimento vertical, uma vez que ele sai de y 2 até chegar em y 3 . Vamos usar a equação abaixo, do movimento acelerado...

y 3 = y 2 + v 2 y t 3 - t 2 + 1 2 a y ( t 3 - t 2 ) 2  

Onde a aceleração a y , é na verdade, a aceleração da gravidade, com sinal negativo porque aponta para baixo e o sentido positivo do nosso referencial é para cima.

Quanto a velocidade v 2 y , precisamos levar em consideração o ângulo de lançamento, que é de 45 ° .

Ficamos então, com...

2,0   m = ( 2,0   m ) + ( 8,091 sen ⁡ 45 °   m / s ) t 3 - t 2 + 1 2 ( - 9,8   m / s ² ) ( t 3 - t 2 ) 2  

( 8,091 sen ⁡ 45 °   m / s ) t 3 - t 2 = 1 2 ( 9,8   m / s ² ) ( t 3 - t 2 ) 2  

( 8,091 sen ⁡ 45 °   m / s ) - 1 2 ( 9,8   m / s ² ) t 3 - t 2 =

t 3 - t 2 = 8,091 sen ⁡ 45 °   m / s 4,8   m / s ²

t 3 - t 2 = 1,168   s

Passo 4

Na direção horizontal, em x , o nosso movimento é uniforme. Sendo assim, usemos a equação abaixo...

x 3 = x 2 + v 2 x t 3 - t 2

x 3 - x 2 = v 2 x t 3 - t 2

Bom! Pelo que vemos na figura do P a s s o   1 , ( x 3 - x 2 ) é justamente a distância d que pede o enunciado. Desse jeito,

x 3 - x 2 = d = v 2 x t 3 - t 2

Qunato à velocidade v 2 x ... Ela é a componente horizontal da velocidade de lançamento em ( 2 ) , dada pelo produto de v 2 pelo cosseno do ângulo de lançamento.

Assim fica fácil obter nossa resposta! Ela é igual à...

d = v 2 x t 3 - t 2

d = ( 8,091 cos ⁡ 45 °   m / s ) 1,168   s

d = 6,68   m

Pronto! Terminamos aqui!

Resposta

d = 6,68   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

32 . || a. Na F I G U R AE X 10.32 , qual é o valor mínimo de velocidade que uma partícula de 100g necessita ter no ponto A para poder chegar ao ponto B ? b . Qual é o mínimo valor de velocidade que u
44 . ||| Um cofre de 1.000k g encontra-se 2,0m acima de uma mola dura e resistente quando o cabo que o sustenta se rompe. O cofre colide com a mola e a comprime em 50c m . Qual é a constante elástica
47 . || Uma panela de massa desprezível está suspensa por uma mola presa ao teto. Quando vazia, a panela fica parada a 50c m abaixo do teto. Se um punhado de 100g de argila é suavemente colocado na pa
39 . || A mola da F I G U R AP 10.39 a é comprimida em Δ x . Ela lança o bloco ao longo de uma superfície sem atrito com velocidade v 0 . As duas molas da FIGURA P10.39b são idênticas à da F i g u r a
38. || A mola da FIGURA P10.38a é comprimida em Δ x . Ela lança o bloco com rapidez v 0 ao longo de uma superfície livre de atrito. As duas molas da FIGURA P10.38b são idênticas à mola da Figura P10.3