Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.Problemas adicionais - Ex. 63

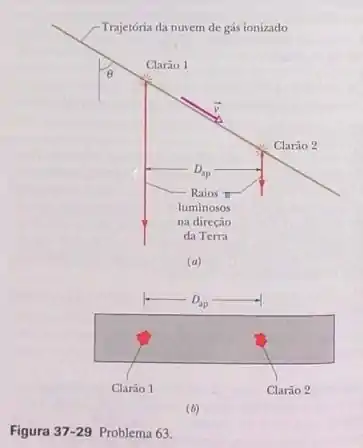
Jatos superluminais. A Fig. 37-29a mostra a trajetória de uma nuvem de gás ionizado expelida por uma galáxia. A nuvem viaja com velocidade constante v → em uma direção que faz um ângulo de θ com a reta que liga a nuvem à Terra. A nuvem emite de tempos em tempos clarões luminosos, que são detectados na Terra. A Fig.37-29a mostra dois desses clarões, separador por um intervalo de tempo t em um referencial estacionário próximo dos clarões. Os clarões aparecem na Fig.37-29b como imagens em um filme fotográfico. A distância aparente D a p percorrida pela nuvem entre os dois clarões é a projeção da trajetória da nuvem em uma perpendicular à reta que liga a nuvem à Terra. O intervalo de tempo aparente T a p entre os dois eventos é a diferença entre os tempos de chegada dos raios luminosos associados aos dois clarões. A velocidade aparente da nuvem é, portanto, V a p = D a p / T a p . Quais são os valores de (a) D a p ; (b) T a p ? A resposta deve ser expressa em função de v ,   t   e   θ . (c) Determine V a p para v = 0,98 ⋅ c e θ = 30,0 º . Quando os jatos superluminais (mais velozes que a luz) foram descobertos, pareciam violar a teoria da relatividade restrita, mas logo os astrônomos se deram conta de que podiam ser explicados pela geometria da situação (Fig. 37-29a) sem necessidade de supor que havia corpos se movendo mais depressa que a luz.

Passo 1

Para resolvermos esse problema vamos usar apenas relações trigonométricas da geometria do problema, onde vamos descobrir qual a distância entre os clarões a partir do ângulo dado assim como o tempo entre os eventos.

Passo 2

  1. Temos, pelo esquema dado na figura, que a distância pode ser obtida através do seno do ângulo estabelecido, uma vez que o ângulo pode ser projetado nos raios luminosos que vão em direção a Terra. Assim, nossa distância aparente será

    2. D a p = L ⋅ sin ⁡ θ

    Sendo L o tamanho da hipotenusa que separa os dois eventos e que pode ser escrita por

    L = v ⋅ t

    Assim:

    D a p = v ⋅ t ⋅ sin ⁡ θ

    Passo 3

  2. Sabemos que o clarão 1 é emitido alguns momentos antes que o segundo, assim vamos dizer que ele tem um tempo t . Temos também que o primeiro clarão tem que percorrer uma distância h maior que o segundo clarão, onde h pode ser escrito por

    3. h = v ⋅ t ⋅ cos ⁡ θ

    E o tempo necessário para percorrer essa distância é dada por t ' = h c . Assim, temos que o tempo aparente será dado pela diferença entre os dois tempos. Portanto

    T a p = t - t ' = t - v ⋅ t ⋅ cos ⁡ θ c = t ⋅ 1 - v c ⋅ cos ⁡ θ

    Passo 4

  3. Dada a relação V a p = D a p / T a p , temos que para v = 0,980 ⋅ c e θ = 30 º teremos a seguinte velocidade aparente

V a p = D a p T a p = v c ⋅ sin ⁡ θ 1 - v c ⋅ cos ⁡ θ ⋅ c = 0,980 ⋅ sin ⁡ 30,0 º 1 - 0,980 ⋅ cos ⁡ 30,0 º ⋅ c = 3,24 ⋅ c

Resposta

a) D a p = v ⋅ t ⋅ sin ⁡ θ

b) T a p = t ⋅ 1 - v c ⋅ cos ⁡ θ

c) V a p = 3,24 ⋅ c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que os dois raios da figura atinjam simultaneamente o solo em relação a um observador dentro do trem. Mostre que esses eventos não ocorrem simultaneamente em relação a um observador situado no
Duas fontes idênticas de luz monocromática, de frequência ν o , afastam-se uma da outra (fig.) com velocidades v e - v num referencial inercial ( S ). Qual a frequência ν de uma das fontes, quando obs
Quais das seguintes afirmativas são postulados fundamentais da teoria da relatividade especial? Mais de uma afirmativa pode estar correta. (a) A luz se move através de uma substância chamada éter. (a)
Um astronauta está viajando em uma nave espacial no espaço em linha reta a uma velocidade constante de 0,500c. Quais dos seguintes efeitos ele experimentaria? (a) Sentir-se-ia mais pesado. (b) Acharia
Conforme um carro segue por uma estrada, movendo- -se a uma velocidade v , distanciando-se do observador no solo, quais das seguintes afirmativas são verdadeiras sobre a velocidade medida do feixe de