Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.Problemas adicionais - Ex. 64
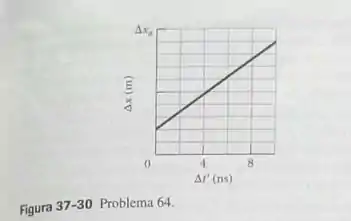
O referencial passa pelo referencial com uma certa velocidade, como na Fig. 37-9. Os eventos 1 e 2 estão separados por uma distância de acordo com um observador em repouso no referencial . A Fig. 37-30 mostra a distância entre os dois eventos de acordo com um observador em repouso no referencia em função de , para A escala do eixo vertical é definido por . Qual é o valor de ?
Passo 1
Para resolvermos esse problema vamos fazer uma análise do gráfico e iremos comparar com a Eq. 1 da tabela 37-2, como também manipulações algébricas e analogias com equações de reta
Passo 2
Temos que a equação que rege essa curva é dada por. Podemos fazer uma analogia com a equação de reta onde teríamos um termo onde seria a inclinação da reta e outro termo que seria a intersecção com o “eixo ”. Assim, teríamos a seguinte equação
Supondo que a escala do gráfico na direção seja de para cada quadrado, temos que a inclinação da reta seria
Assim, igualando a esse valor e manipulando o para isolarmos a velocidade, chegamos que
E para temos que
Agora que temos , podemos analisar a intersecção com o eixo para encontrarmos . Pela primeira análise que fizemos, chegamos que
Assim, temos que