Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 69
Jill acaba de sair de seu carro no estacionamento de uma confeitaria. O estacionamento fica em uma colina e tem inclinação de . Cinquenta metros colina abaixo, a partir de Jill, uma velhinha solta sem querer um carrinho de supermercado carregado. O carrinho, com rodas desprovidas de atrito, começa a rolar em linha reta colina abaixo. Jill imediatamente começa a correr atrás dele com sua aceleração máxima de . Que distância rolará o carrinho antes que Jill o alcance?
Passo 1
Se liga! Para resolver esta questão precisaremos escrever a posição horária para Jill e o carrinho da senhora. Se liga na figura!
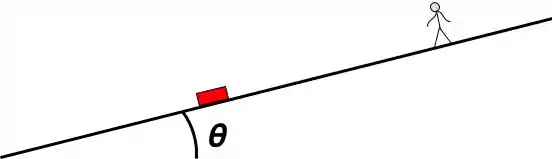
Observe que o carrinho desce devido a ação da gravidade. Como no plano inclinado, devido a configuração usada, a aceleração é dada por
Temos que a aceleração do carrinho, será
Como a velocidade inicial do carrinho é ZERO, temos
Passo 2
Agora podemos escrever a função horária para Jill. Como ele está 50 metros atrás do carrinho, parte do repouso com aceleração é de , temos
Passo 3
Já que queremos a distância que o carrinho percorre até que Jill o alcance, precisamos saber quando Jill vai alcançá-lo. Sendo assim, precisaremos igualar as posições
Passo 4
Substituindo esse valor na equação (1), encontramos a distância percorrida pelo carrinho