Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 5

Uma lâmina de vidro de faces planas paralelas tem um índice de refração n e espessura h . Um raio de luz incide sobre ela com ângulo de incidência θ 1 ,. Mostre que o raio transmitido através da lâmina é paralelo ao raio incidente. A distância perpendicular d entre o raio transmitido e o prolongamento do raio incidente chama-se desvio lateral. Calcule d em função de n ,   h   e θ 1 .

Passo 1

Opa!! Vamoslá!

Pra gente mostrar que o raio incidente e o raio transmitido são paralelos devemos mostrar que eles possuem a mesma inclinação, ou seja, o mesmo ângulo.

Vamos fazer um desenho:

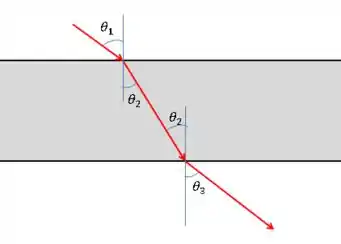
Vamos aplicar a lei de Snell na interface de cima.

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

Agora, na interface de baixo:

n 2 sen ⁡ θ 2 = n 1 sen ⁡ θ 3

Mas podemos substituir uma na outra:

n 1 sen ⁡ θ 1 = n 1 sen ⁡ θ 3

Opa!

Temos

sen ⁡ θ 1 = sen ⁡ θ 3

Então

θ 1 = θ 3

Portanto, os raios são paralelos.

Passo 2

Agora vamos calcular o desvio lateral.

Vamos desenhar e ver quem é esse cara.

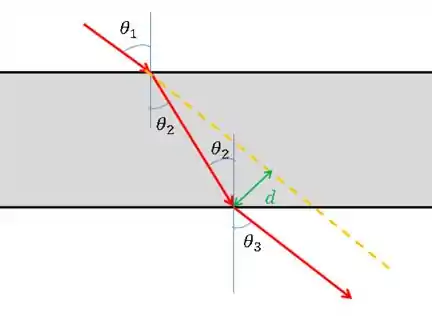
Beleza, agora vamos calcular esse cara. Pra isso, vamos começar chamando a distância que o raio percorre dentro da lâmina de m .

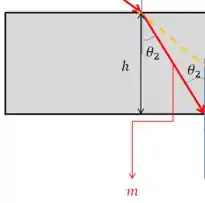
Vemos que cos ⁡ θ 2 = h m

Então

m = h cos ⁡ θ 2

Ok. Vamos marcar uns ângulos agora.

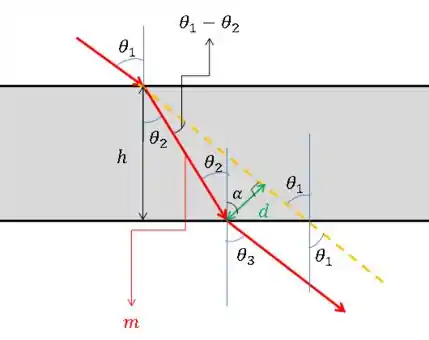
Vamos olhar para o triângulo formado dentro dentro da película. A soma dos ângulos internos vale 180 ° , então

θ 1 - θ 2 + 90 ° + α + θ 2 = 180 °

α = 90 ° - θ 1

Beleza!

Podemos achar o d calculando o seno do ângulo θ 1 - θ 2

sen ⁡ θ 1 - θ 2 = d m

Mas o m   vale

m = h cos ⁡ θ 2

Então

sen ⁡ θ 1 - θ 2 = d m

sen ⁡ θ 1 - θ 2 = d cos ⁡ θ 2 h

Pela regra da soma de arcos, temos

sen ⁡ θ 1 - θ 2 = sen ⁡ θ 1 cos ⁡ θ 2 - sen ⁡ θ 2 cos ⁡ θ 1

Então

sen ⁡ θ 1 - θ 2 = d cos ⁡ θ 2 h

sen ⁡ θ 1 cos ⁡ θ 2 - sen ⁡ θ 2 cos ⁡ θ 1 = d cos ⁡ θ 2 h

Assim

d = h sen ⁡ θ 1 cos ⁡ θ 2 - sen ⁡ θ 2 cos ⁡ θ 1 cos ⁡ θ 2

d = h sen ⁡ θ 1 - sen ⁡ θ 2 cos ⁡ θ 1 cos ⁡ θ 2

Mas olha só,pela lei de Snell, na interface de cima, temos:

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

Então

sen ⁡ θ 2 = n 1 n 2 sen ⁡ θ 1

Substituindo:

d = h sen ⁡ θ 1 - sen ⁡ θ 2 cos ⁡ θ 1 cos ⁡ θ 2

d = h sen ⁡ θ 1 - n 1 n 2 sen ⁡ θ 1 cos ⁡ θ 1 cos ⁡ θ 2

Então

d = h sen ⁡ θ 1 1 - n 1 n 2 cos ⁡ θ 1 cos ⁡ θ 2

Agora, temos que escrever o cos ⁡ θ 2 em termos de θ 1 , porque o enunciado pediu.

Pra isso, vamos usar a lei de snell novamente:

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

Vamos elevar isso ao quadrado:

n 1 2 sen 2 ⁡ θ 1 = n 2 2 sen 2 ⁡ θ 2

Usando a relaçãotrigonométrica fundamental, sabemos que:

sen 2 ⁡ θ 2 = 1 - cos 2 ⁡ θ 2

Então

n 1 2 sen 2 ⁡ θ 1 = n 2 2 sen 2 ⁡ θ 2

n 1 2 sen 2 ⁡ θ 1 = n 2 2 ( 1 - cos 2 ⁡ θ 2 )

Então

cos ⁡ θ 2 = 1 - n 1 2 n 2 2 sen 2 ⁡ θ 1

Show!

Vamos voltar lá para a equação do d .

d = h sen ⁡ θ 1 1 - n 1 n 2 cos ⁡ θ 1 cos ⁡ θ 2

d = h sen ⁡ θ 1 1 - n 1 n 2 cos ⁡ θ 1 1 - n 1 2 n 2 2 sen 2 ⁡ θ 1

Considerando o meio 1 como o ar, temos que n 1 = 1 e n 2 o enunciado chamou de n , então:

d = h sen ⁡ θ 1 1 - 1 n cos ⁡ θ 1 1 - 1 n 2 sen 2 ⁡ θ 1

d = h sen ⁡ θ 1 1 - cos ⁡ θ 1 n 2 - sen 2 ⁡ θ 1

Resposta

d = h sen ⁡ θ 1 1 - cos ⁡ θ 1 n 2 - sen 2 ⁡ θ 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um raio de luz incide sobre a superfície plana que separa duas placas finas de vidro com índices de refração 1,70 e 1,56 . O ângulo de incidência é 62 ° , e o raio provém da placa que possui índice de
Uma placa de vidro horizontal com faces paralelas de índice de refração igual a 1,52 está em contato com a superfície da água em um tanque. Um raio proveniente do ar acima da placa forma um ângulo de
Em um material com um índice de refração n , um raio de luz possui uma frequência f . um comprimento de onda λ e uma velocidade v . Qual é a frequência, o comprimento de onda e a velocidade dessa luz
A luz passa por três blocos paralelos de espessuras e índices de refração diferentes. A luz incide no primeiro bloco e, finalmente, refrata para dentro do terceiro bloco. Mostre que o bloco do meio nã