Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 59
Lei de Gauss para a gravitação. A força gravitacional entre duas massas puntiformes separadas por uma distância é proporcional a , tal como no caso da força elétrica entre duas cargas puntiformes. Em virtude dessa semelhança entre uma força gravitacional e uma força elétrica, também existe uma lei de Gauss para a gravitação. Seja a aceleração da gravidade produzida por uma massa puntiforme na origem, de modo que . Considere uma superfície gaussiana esférica com raio , centralizada sobre essa massa puntiforme, e demonstre que o fluxo de através dessa superfície é dado por
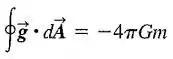
Usando as mesmas etapas lógicas adotadas na Seção para deduzir a lei de Gauss para um campo elétrico, demonstre que o fluxo de através de qualquer superfície fechada é dado por
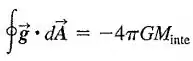
Em que é a massa total no interior da superfície fechada.
Passo 1
Utilizando a lei de Gauss para a gravitação, o fluxo de por uma superfície gaussiana de raio será:
Como a superfície esférica é uma superfície fechada, temos que:
Portanto:
Passo 2
A partir desse resultado, podemos fazer uma comparação.
Se para a lei de Gauss para uma carga puntiforme o fluxo elétrico sobre uma superfície gaussiana depende apenas da carga total envolvida pela superfície, para o caso gravitacional ocorre o mesmo caso, tal que no lugar da carga teremos uma massa total sendo envolvida pela superfície gaussiana.
Logo, considerando uma superfície fechada arbitrária, o fluxo gravitacional que passa por ela depende da massa total no seu interior, ou seja:
Resposta
Ei, a resposta está no passo a passo :)