Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 28.Exercícios e Problemas - Ex. 18
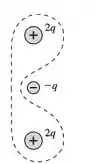
A FIGURA EX28.18 mostra três cargas. Faça desenhos das cargas sobre uma folha de papel. Em seguida, desenhe uma secção transversal bidimensional de uma superfície fechada tridimensional através da qual o fluxo elétrico seja igual a:
a)
b)
c)
d)
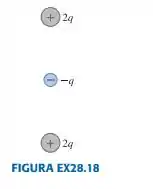
Passo 1
Faaaaaala, galera... Tranquileba??
Sabemos, pelo princípio pela lei de gauss para fluxo elétrico, que para qualquer superfície fechada:
Passo 2
Para (a):
Para que façamos o fluxo elétrico ser igual ao pedido em(a), ou seja, , devemos fazer:
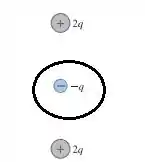
Para (b):
Para que façamos o fluxo elétrico ser igual ao pedido em(a), ou seja, , devemos fazer:
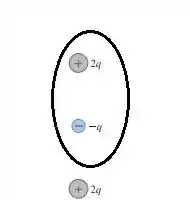
Passo 3
Para (c):
Para que façamos o fluxo elétrico ser igual ao pedido em(a), ou seja, , devemos fazer:
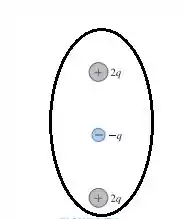
Para (d):
E para a quarta equação, ou seja, :
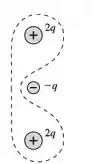
Resposta
a)
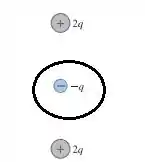
b)
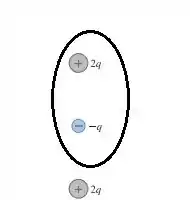
c)
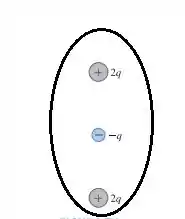
d)
Exercícios de Livros Relacionados
49 . Uma esfera oca isolante possui raio interno a e raio externo b . No interior do material isolante, a densidade volumétrica de carga é dada por ρ r = α / r , em que α é uma constante positiva. ( a
61 . Uma distribuição de cargas, de raio R = 6,00m m , possui densidade volumétrica de carga ρ não uniforme. A Figura P 22.61 mostra ρ em função da distância r do centro da distribuição de cargas. Cal
Uma esfera de raio R possui uma carga Q . A intensidade de campo elétrico a uma distância rR é E i . Qual é a razão E f / E i entre as intensidades de campo final e inicial se (a) Q diminui pela metad
Um excesso de 55,3 milhões de elétrons encontra-se dentro de uma superfície fechada. Qual é o fluxo elétrico resultante através da superfície?
As cargas q 1 = - 4 Q e q 2 = + 2 Q estão localizadas em x = - a e x = + a , respectivamente. Qual é o fluxo elétrico resultante através de uma esfera de raio2 a centrada: na origem do sistema de coor