Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.7 - Ex. 23
Uma linha infinita de cargas produz um campo de módulo a uma distância de . Calcule a densidade linear de cargas.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui o que queremos saber basicamente é a densidade linear de carga produzido por uma linha infinita de carga.
Vamos considerar uma superfície cilíndrica infinita ao redor dessa linha infinita de cargas:
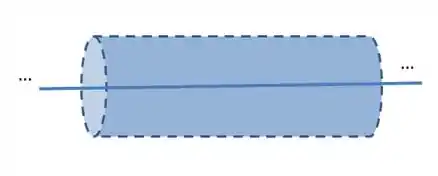
Pela Lei de Gauss, sendo uma pequena unidade de superfície do cilindro considerado:
Passo 2
Nesse caso, a carga interna à região pontilhada é dada por:
, sendo a densidade linear de cargas.
Abrindo uma unidade desse cilindro em um retângulo, a gente encontra que, supondo o raio do cilindro igual a :
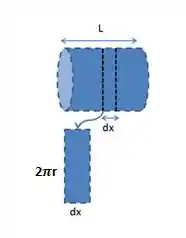
Daí:
Então
Isolando :
Resposta
Exercícios de Livros Relacionados
A Fig. 23-38 é uma seção de uma barra condutora de raio R 1=1,30m m e comprimento L=11,00m no interior de uma casca coaxial, de paredes finas, de raio R 2=10,0 R 1 e mesmo comprimento L . A carga da b
A Fig. 23-38 é uma seção de uma barra condutora de raio R 1 = 1,30m m e comprimento L = 11,00m no interior de uma casca coaxial, de paredes finas, de raio R 2 = 10,0 R 1 e mesmo comprimento L . A carg
Um cilindro maciço, longo, não condutor, com 4,0c m de raio, possui uma densidade volumétrica de cargas não uniforme ρ que é função da distância radial r a partir do eixo do cilindro: ρ=Ar 2 . Se A=2,
Um elétron é arremessado na direção do centro de uma placa metálica que possui uma densidade superficial de cargas de - 2,0 × 10 - 6C / m 2 . Se a energia cinética inicial do elétron é 1,60 ×10 - 17J
Duas grandes placas de metal com 1,0m 2 de área são mantidas paralelas a 5,0c m de distância e possuem cargas de mesmo valor absoluto e sinais opostos nas superfícies internas. Se o módulo E do campo