Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.7 - Ex. 32
Um cilindro maciço, longo, não condutor, com de raio, possui uma densidade volumétrica de cargas não uniforme que é função da distância radial a partir do eixo do cilindro: . Se , determine o módulo do campo elétrico (a) para ; (b) para
Passo 1
Faaaaala galerinha, animados?
Então bora laa ...
Nós queremos achar o campo elétrico em dois raios distintos, um interno ao cilindro e outro externo, ok?
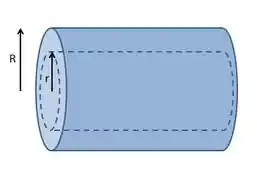
Quando estamos falando de uma situação interna ao cilindro do problema!! Então vamos considerar a superfície gaussiana como sendo um cilindro de e comprimento
Passo 2
Para calcular a carga dentro do cilindro podemos usar a relação:
Onde é uma unidade infinitesimal de carga interna e a unidade pequenina de volume!!
Para um cilindro nós temos que:
Substituindo:
E lembrando que:
Então:
Para encontrar a carga interna nós vamos integrar:
Shooow !! Achamos algo muito importante, mas ainda não terminamos !!
Passo 3
Acabamos de achar a carga interna a uma distância do eixo central e agora, só falta usarmos a Lei de Gauss:
Para resolver a integral é importante nós lembrarmos que, como o campo elétrico aponta na direção radial nós só teremos fluxo na área lateral do cilindro, ou seja, de 0 até L:
E igualando:
Passo 4
Substituindo que achamos no Passo 1:
Agora ficou top demais, basta nós usarmos:
Substituindo:
Passo 5
Na letra (b) temos , certo?
Já sabemos do Passo 2 que:
E pelo Passo 1 nós achamos a carga interna ao cilindro:
Substituindo para achar o campo:
E colocando os dados:
E fechamos mais umaa !!