Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 30.1 - Ex. 56
Um longo solenoide com n voltas por unidade de comprimento conduz uma corrente que aumenta linearmente com o tempo. O solenoide tem raio , comprimento a corrente nas voltas é dada por .
(a)Determine o campo elétrico induzido a uma distância do eixo central do solenoide.
(b)Determine a magnitude, a direção e o sentido do vetor Poynting S em (no interior das voltas do solenoide).
(c)Calcule o fluxo para dentro do solenoide e mostre que o fluxo e igual a taxa de aumento da energia magnética no interior do solenoide.
Passo 1
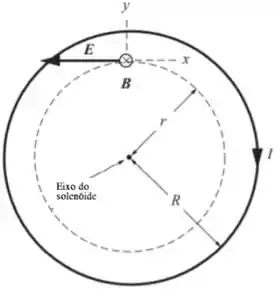
Uma vista final do solenóide é mostrada no diagrama. Seja a corrente no sentido horário e escolha um sistema de coordenadas no qual a direção +x é tangente às superfícies cilíndricas concêntricas com o eixo do solenóide. Note que a direção +z está fora do plano do diagrama. Podemos usar a lei de Faraday para expressar o campo elétrico induzido a uma distância do eixo do solenóide em termos da taxa de variação do fluxo magnético e para expressar B em termos da corrente nos enrolamentos do solenóide. Podemos usar os resultados de (a) para encontrar o vetor de Poynting na superfície cilíndrica r = R apenas dentro dos enrolamentos do solenóide . Na Parte (c), usaremos a definição de fluxo e a expressão para a energia magnética em uma determinada região para mostrar que o fluxo de 
para o solenóide é igual à taxa de aumento da energia magnética dentro do solenóide.
Passo 2
Letra a:
Aplique a lei de Faraday a um caminho circular de raio para relacionar a magnitude do campo elétrico induzido à magnitude da taxa de mudança do fluxo magnético:
Resolvendo, temos:
Expresse a força do campo magnético dentro de um solenóide longo:
O fluxo magnético através de um círculo de raio r é:
Substitua por na equação (1) e simplifique para obter:
A direção de é tal que produz uma fem que se opõe ao aumento da corrente, então se a corrente for no sentido horário, então está na direção oposta e:
onde é um vetor unitário tangente aos círculos concêntricos com o eixo do solenóide.
Passo 3
Letra b:
Expresse em r = R:
Como é um vetor que aponta em direção ao eixo do solenóide, também podemos escrever como:
Passo 4
Letra c:
Considere uma superfície cilíndrica de comprimento L e raio R. Como aponta para dentro, a energia fluindo para o solenóide por unidade de tempo é:
Expresse a energia magnética no solenoide
Observações: A igualdade das duas taxas de fluxo é uma declaração da conservação de energia.
Resposta
- A igualdade das duas taxas de fluxo é uma declaração da conservação de energia.