Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 55
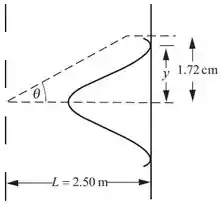
Três fendas, cada uma separada da fenda ao lado por , são iluminadas no máximo central de intensidade por uma fonte de luz coerente com comprimento de onda igual a . As fendas são extremamente estreitas. Um anteparo é colocado a das fendas. A intensidade é . Considere a posição a do máximo central. (a) Desenhe um diagrama de fasores adequado para a adição das três ondas harmônicas naquela posição. (b) Do diagrama de fasores, calcule a intensidade da luz naquela posição.
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
Certo! Observe que, podemos encontrar a constante de fase a partir da geometria do diagrama à direita. Usando o valor de encontrado desta forma, podemos expressar a intensidade no ponto a da linha central em termos da intensidade na linha central. Na linha de centro, a amplitude da onda resultante é vezes a de cada onda individual e a intensidade é vezes a de cada fonte agindo separadamente.
Passo 2
Certo! Expressando para as fendas adjacentes:
Para , :
Substituindo, vamos obter
Substituindo numericamente, temos
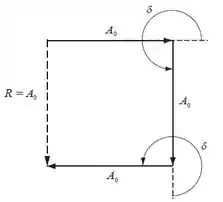
Os três fasores, separados por , são mostrados no diagrama à direita. Note que eles formam três lados de um quadrado. Consequentemente, sua soma, mostrada como o resultante, é igual à magnitude de um dos fasores.
Passo 3
Já no item b) Expressamos a intensidade no ponto a da linha central:
Como :
Assim,
Substituindo numericamente, encontraremos
Passo 4
Pronto! Finalizamos a questão 😊. Nos vemos na próxima questão. OK? Até mais.