Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 36
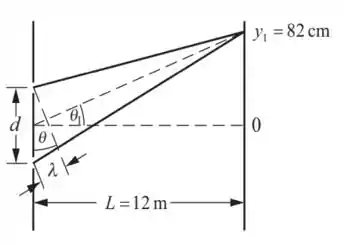
Luz com comprimento de onda de 633 nm de um laser de hélio-neônio incide normalmente em um plano contendo duas fendas. O primeiro máximo de interferência está a 82 cm do máximo central no anteparo que está a 12 m de distância.
a) Determine a separação entre as fendas.
b) Quantos máximos de interferência é possível, em princípio, observar?
Passo 1
Meus amigos e minhas amigas!
Podemos usar apenas geometria para encontrar a separação das fendas. Agora, para encontrar quantos máximos de interferência são possíveis de observar podemos aplicar a equação que descreve a interferência entre duas fendas com :
Passo 2
No item a):
Para o triângulo de lados e L:
Entretanto, queremos encontrar :
Como , podemos aproximar:
Passo 3
Agora, por fim, o item b):
Como queremos saber o “máximo” de uma equação trigonométrica, precisamos usar:
Então:
Aplicando o valor encontrado anteriormente para encontrar o valor inteiro de m:
Entretanto, não é nossa resposta final, já que esse é o valor encontrado para apenas um lado ao redor do centro: