Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 40

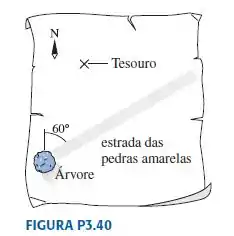
O mapa do tesouro da FIGURA P3.40 fornece as seguintes orientações para o tesouro enterrado: “Parta do velho carvalho, caminhe 500 passos para o norte e, depois, 100 passos para o leste. Cave”. Mas quando você começa a caminhada, depara-se com um dragão furioso exatamente ao norte da árvore de partida. A fim de evitar a fera, você pega uma longa estrada de pedras amarelas 60° a leste de norte. Depois de dar 300 passos, você percebe a entrada de uma trilha na floresta. Que orientação você deveria tomar e que distância deveria percorrer a fim de chegar ao tesouro?

Passo 1

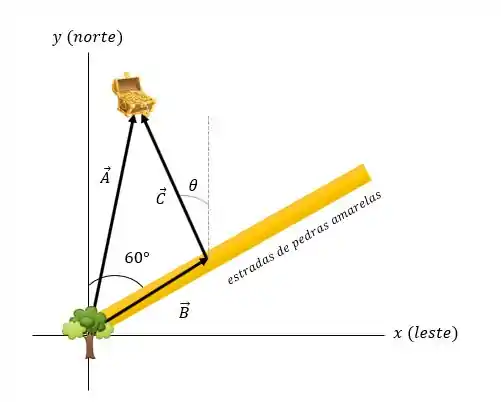
Bom galerinha, aqui vamos estabelecer um sistema de coordenadas com origem na árvore e com o e i x o   x apontando para o leste. Deixei que A →   seja um vetor de deslocamento iretamente da árvore para o tesouro.

O vetor A →   é A → = ( 100 i ^ + 500   j ^ ) passos. Isso descreve o deslocamento que você sofreria caminhando para o norte 500 passos e depois para o leste 100   passos. Em vez de, você segue a estrada por 300 passos e sofre deslocamento

B → = 300   s e n   60 ° i ^ + 300 cos ⁡ 60 ° j ^ p a s s o s = 260 i ^ + 150 ⁡ j ^   p a s s o s

Passo 2

Agora seja C o vetor de deslocamento da sua posição para o tesouro. Da figura: A → = B → + C → .

Portanto, o deslocamento que você precisa para alcançar o tesouro é:

C → = A → - B → = - 160 i ^ + 350 j →   p a s s o s .

Passo 3

Se θ é o ângulo medido entre C → e o e i x o   y ,

θ = tan - 1 ⁡ 160 350 = 24,6 °

Você deve seguir 24,6   ° a oeste do norte. Você precisa caminhar

C = C x 2 + C y 2 = 385   p a s s o s  

para chegar ao tesouro.

Resposta

24,6   ° a oeste do norte

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O vetor posição de um próton é inicialmente r →=5,0 i →- 6,0 j →+ 2,0 k → e depois se torna r → =- 2,0 i →+6,0 j →+ 2,0 k → , com todos os valores em metros. (a) Qual é o vetor deslocamento do próton?
A Fig. 4-61 mostra a trajetória seguida por um gambá bêbado em um terreno plano, de um ponto inicial i até um ponto final f Os ângulos são θ 1 =30,0 ° , θ 2 =50,0 ° e θ 3=80,0 ° ; as distâncias são d
Você foi sequestrado por estudantes de ciência política (que estão aborrecidos porque você declarou que ciência política não é ciência de verdade). Embora esteja vendado, você pode estimar a velocidad
Na Fig. 4-49, uma estação de radar detecta um avião que se aproxima, vindo do Leste. Quando é observado pela primeira vez, o avião está a uma distância d 1 = 360m da estação e θ 1 = 40 ° acima do hori
A velocidade de uma partícula é dada por v x = 7,0 m s 3 t 2 - 5,0 m s . Se a partícula está na origem em t 0 = 0 , encontre a função x ( t ) da posição.