Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 44

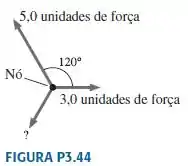
A FIGURA P3.44 mostra três cordas amarradas juntas por um nó. Um dos colegas puxa uma corda com 3,0 unidades de força, e outro puxa uma segunda corda com 5,0 unidades de força. Com que força e com qual orientação você deve puxar a terceira corda para impedir que o nó se mova?

Passo 1

Trataremos o nó na corda como uma partícula em equilíbrio estático.

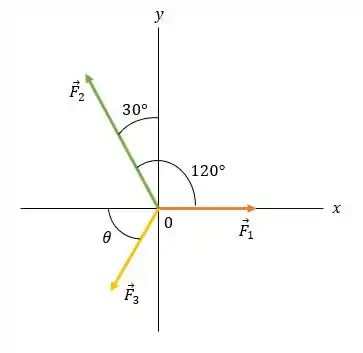
Nós conhecemos . E queremos encontrar e .

Passo 2

Expressando os vetores usando vetores unitários, temos:

Desde que , nós podemos escrever da seguinte forma:

A magnitude de é dada por:

O ângulo que é :

e está abaixo do eixo negativo.

Passo 3

O vetor resultante tem ambos os componentes negativos e, portanto, está no quadrante III. Sua magnitude e direção são razoáveis. Observe o sinal de menos que inserimos manualmente com a força .

Resposta

na direção de abaixo do eixo negativo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Jack e Jill sobem uma colina correndo a 3,0 m/s. O componente horizontal do vetor velocidade de Jill vale 2,5 m/s.a. Qual é o ângulo de inclinação da colina?b. Qual é o componente vertical da velocida

Um avião a jato está voando horizontalmente com uma rapidez de 500 m/s sobre uma colina com 3 % de inclinação para cima (i. e., ela “se eleva” 3 % do que percorre na horizontal). Qual é o componente d

Uma pinha cai diretamente para baixo a partir de um pinheiro que cresceu com inclinação de 20 ° . A pinha bate no solo com rapidez de 10 m/s. Qual é o componente da velocidade de impacto da pinha (a)

São exercidas três forças sobre um objeto localizado sobre o piso inclinado da FIGURA P3.45. As forças são expressas em newtons (N). Considerando as forças como vetores:a. Qual é o componente da força

A velocidade de lançamento de um projétil é cinco vezes maior que a velocidade na altura máxima. Determine o ângulo de lançamento θ 0 .