Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 139
Uma máquina de Atwood, cuja polia é sem massa e sem atrito e cujo cordão é sem massa, tem um corpo de suspenso de um lado e um corpo de 4,00 kg suspenso do outro lado. (a) Qual é a rapidez de cada corpo depois deles terem sido simultaneamente largados do repouso? (b) Neste momento, qual é a velocidade do centro de massa dos dois corpos? (c) Neste momento, qual é a aceleração do centro de massa dos dois objetos?
Passo 1
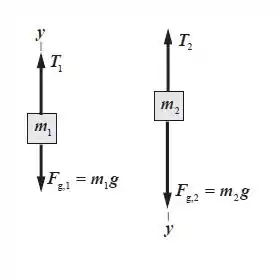
As forças que atuam nos objetos 2,00 kg () e 4,00 kg () são mostradas no diagrama do corpo livre abaixo. Note que os dois objetos têm a mesma aceleração e velocidades comuns. Nós podemos usar a equação da aceleração constante e a Segunda Lei de Newton na análise do movimento desses objetos.
Passo 2
Item (a)
Usando a equação da aceleração constante para relacionar a velocidade do
objetos para sua aceleração comum:
Considerando :
Aplicando no objeto de massa :
Aplicando no objeto de massa :
Como somando as duas equações acima:
Substituindo na equação da velocidade:
E, por fim, substituindo pelos valores numéricos para encontrar :
Passo 3
Item (b)
A velocidade do centro de massa é dado por:
Substituindo por valores numéricos para encontrar :
Então, a velocidade do centro de massa é para baixo.
Passo 4
Item (c)
A aceleração do centro de massa é dada por:
Substituindo por que encontramos anteriormente e simplificando:
Agora, substituindo por valores numéricos:
Então, a aceleração do centro de massa é para baixo.