Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.11 - Ex. 71

O próton 1, com uma velocidade de 500   m / s , colide elasticamente com o próton 2, inicialmente em repouso. Depois do choque, os dois prótons se movem em trajetórias perpendiculares, com a trajetória do próton 1 fazendo 60 ° com a direção inicial. Após a colisão, qual é a velocidade escalar (a) do próton 1 e (b) do próton 2?

Passo 1

Oi, galerinha! Tudo bom? Segundo o enunciado a direção do movimento do próton 1 é θ   =   + 60 ° e a direção do movimento do próton 2 , por sua vez ,é ∅ =   – 30 ° , uma vez que suas trajetórias são perpendiculares. Vamos desenhar para visualizar melhor!

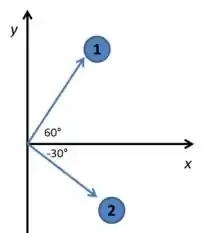
Aplicando a lei de conservação do momento linear às componentes   x e y , temos que :

p a r a   c o m p o r a n e n t e   x →   m 1 v 1 = m 1 v 1 ' cos ⁡ 60 ° + m 2 v 2 ' cos ⁡ 30 °

p a r a   a   c o m p o n e n t e   y → 0 = m 1 v 1 ' sen ⁡ 60 ° + m 2 v 2 ' sen ⁡ 30 °

Como temos que que v 1   =   500   m / s , temos duas equações e duas incógnitas ( v 1 ' e v 2 ' ).Além disso, como m 1   =   m 2 , as massas se cancelam e não aparecem na solução.

Combinando as equações acima e explicitando v 2 ' , obtemos que :

v 2 ' = v 1 sen ⁡ 60 ° ( s e n 60 °   c o s - 30 ° )   – c o s 60 °   s e n - 30 °

v 2 ' = 500 m s s e n 60 ° 1 = 433 m / s

Passo 2

Utilizando raciocínio anállogo ao item anterior e explicitando v 1 ' , obtemos que :

v 1 ' = 500 m s sen ⁡ - 30 ° 1 = 250 m s

Resposta

v 2 ' = 433 m / s

v 1 ' = 250 m s

Tranquilo galera? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na vista superior da Fig. 9-54, uma bola de 300g com uma velocidade escalar v de 6,0m / s se choca com uma parede com um ângulo θ de 30 ° e ricocheteia com a mesma velocidade escalar e o mesmo ângulo.
O lagarto basilisco é capaz de correr na superfície da água (Fig. 9-52). Em cada passo, o lagarto bate na água com a pata e a mergulha tão depressa que uma cavidade de ar se forma acima da pata. Para
A Fig. 9-53 mostra um gráfico aproximado do módulo da força F em função do tempo t para uma colisão de uma Superbola de 58   g com uma parede. A velocidade inicial da bola é 34   m / s , perpendicular
Um disco de metal de 0,25   k g está inicialmente em repouso em uma superfície de gelo de atrito desprezível. No instante t = 0 , uma força horizontal começa a agir sobre o disco. A força é dada por F
Um haltere assimétrico consiste em uma barra uniforme de 50c m de comprimento e200g de massa. Em uma extremidade há uma esfera sólida uniforme de 10c m de diâmetro e 500g de massa, e na outra extremid