Exercícios de Conservação da Velocidade e Posição do Centro de Massa - Lista de Exercícios Resolvida
Questão 1
Duas pessoas, de mesma massa , estão de pé e presas às extremidades opostas de uma prancha, de comprimento e massa desprezível, que inicialmente se encontra em repouso sobre uma pista de gelo, como mostrado na figura. A pessoa da direita joga, com certa velocidade horizontal, uma bola de massa em direção à outra pessoa que consegue pegá-la. Despreze os efeitos da resistência do ar e do atrito entre a prancha e a pista de gelo. Para um observador parado na borda da pista:
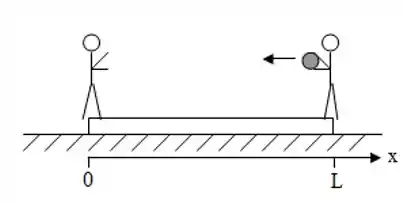
Encontre a equação que descreve a posição do centro de massa () do conjunto prancha + pessoas + bola enquanto a bola vai da direita para a esquerda. Justifique sua resposta com argumentos físicos.
Encontre as equações da velocidade e da posição do centro da prancha (que inicialmente vale ) enquanto a bola vai da direita para a esquerda, em função das massas e da velocidade da bola.
Determine a posição da pessoa da direita, no momento em que a bola é agarrada pela pessoa da esquerda, usando o referencial da figura.
O que acontece com o conjunto prancha + pessoas + bola após que a pessoa da esquerda agarrou a bola? Justifique sua resposta com argumentos físicos.
Ver solução completaQuestão 2
Um projétil é lançado de uma plataforma do ponto e num dado instante após ser lançado ele se fragmenta em dois pedações de massa e , que caem simultaneamente nas posições horizontais e respectivamente. Se o projétil não se fragmentasse o seu alcance seria,
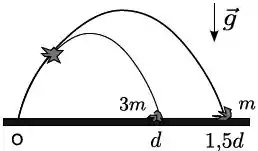
;
;
;
;
;
Ver solução completaQuestão 3
Uma jovem de está em pé sobre uma canoa de e comprimento igual a . Ela caminha a partir de um ponto situado a de uma das extremidades da canoa até atingir a outra extremidade da canoa. Desprezando a resistência da água ao movimento da canoa, qual a distância que a canoa se move nesse processo?

Questão 4
Sobre uma mesa horizontal perfeitamente lisa repousa um sistema formado por duas pequenas massas e , ligadas por uma mola de massa desprezível e que se encontra relaxada. A partir do instante passa a atuar sobre a massa uma força externa constante paralela à mesa, e uma força sobre a massa . Pode-se afirmar que para
O centro de massa do sistema se move ao longo de uma reta
O momento linear total do sistema se conserva
A velocidade do centro de massa é uma função quadrática do tempo
A distância entre as massas e permanece constante
O momento angular total do sistema, referido ao centro de massa, permanece constante
Ver solução completaQuestão 5
Uma granada está em repouso sobre uma mesa horizontal e sem atrito. Num dado instante ela explode em dois fragmentos de massas e velocidades diferentes, onde os fragmentos permanecem movimentando-se sobre a mesa. É possível afirmar que:
A energia cinética é conservada.
A posição do centro de massa das partículas varia com o tempo.
O momento linear total do sistema não é conservado.
A velocidade do centro de massa é nula após a explosão.
Nenhuma das opções acima está correta.
Ver solução completaQuestão 6
Um homem de sentado na popa de uma canoa de e de comprimento, conseguiu trazê-la para uma posição em que está parada, encostada perpendicularmente a um pequeno ancoradouro. Na proa da canoa encontra-se a sua namorada (). Se os dois trocarem de lugar, de que distância a canoa se afastará do ancoradouro?

Questão 7
Um homem de massa está na cesta de um balão de ar quente de massa , que se encontra a uma altura em relação ao solo. Devido a uma força de sustentação do ar conhecida como empuxo, o balão está em repouso em relação ao solo. O homem decide descer do balão usando uma escada de corda de suspensa que toca levemente o solo, conforme a figura.

Se o homem começar a descer pela escada com velocidade (em relação ao balão), qual o sentido e qual a velocidade com que o balão irá se mover em relação ao solo?
Após descer os até o final da escada, o balão terá subido e o homem se encontrará a uma distância entre a base da escada e o solo. Calcule o valor da distância .
Ver solução completaQuestão 8
Um menino, de massa , encontra-se na extremidade esqueda de um barco de comprimento e massa , distribuída homogeneamente. Inicialmente o conjunto, barco e menino, move-se para a direita com velocidade constante , em relação a um referencial inercial colocado na margem do lago. Num dado instante o menino move-se para a extremidade direita do barco, onde permanece. Nesta situação o conjunto move-se com velocidade constante em relação ao mesmo referencial inercial. Desprezando-se o atrito entre o barco e a água, pode-se afirmar, ao fim do processo, que:
- .
- .
- .
- Não se pode determinar , pois não se conhece a força exercida pelo menino sobre o barco.
- Não se pode determinar , pois não se conhece a velocidade inicial do centro de massa do sistema barco-menino.
Questão 9
Uma bola de gude de desloca-se com velocidade de da direita para a esquerda sobre uma pista horizontal sem atrito e colide frontalmente com a outra bola de gude de que se desloca com velocidade de da esquerda para a direita (figura abaixo). (a) Determine o módulo, a direção e o sentido de cada bola de gude depois da colisão (como a colisão é frontal, todos os movimentos ocorrem ao longo da mesma linha reta). (b) Calcule a variação do momento linear (isto é, o momento linear depois da colisão menos o momento linear antes da colisão) para cada bola de gude. Compare os valores obtidos para cada bola de gude. (c) Calcule a variação de energia cinética (isto é, a energia cinética depois da colisão menos a energia cinética antes da colisão) para cada bola de gude. Compare os valores obtidos para cada bola de gude.
Ver solução completaQuestão 10
Entre e , um corpo (1) de massa se move na direção horizontal positiva (), com velocidade . Ele então colide, em , com um corpo em repouso (2), de massa , e os dois corpos saem grudados.
a) Calcule a velocidade dos corpos 1 e 2 após a colisão.
Em , o corpo 2 explode enviando um fragmento de massa com uma velocidade na direção positiva do eixo .
b) Calcule a velocidade do resto do sistema após .
c) Calcule a velocidade do CM total (corpos 1 e 2, inteiros ou não) para , e .
Ver solução completaQuestão 11
Dois amigos estão sentados em um trenó que está voltado para o Norte. O trenó encontra-se inicialmente em repouso sobre uma superfície de gelo sem atrito. A massa do primeiro amigo é igual a , a do segundo é igual a e a massa do trenó é igual a . Em um dado instante os dois amigos decidem pular simultaneamente do trenó. O primeiro amigo salta na direção Leste com módulo da velocidade igual a e o segundo amigo salta na direção Noroeste com módulo da velocidade de . Use caso seja necessário.
a) De quanto se deslocou o centro de massa do sistema após os saltos?
b) Determine a velocidade do trenó (módulo direção e sentido) depois que eles saltam.
c) Faça um diagrama das velocidades finais dos dois amigos e do trenó.
Ver solução completaQuestão 12
Um disco de massa , inicialmente em repouso sobre uma superfície horizontal sem atrito, sofre uma colisão não-frontal com um segundo disco de massa , movendo-se inicialmente ao longo do eixo com velocidade escalar constante . Após a colisão, o segundo disco passa a ter velocidade escalar e sai a um ângulo em relação ao eixo positivo, veja a figura. Use o sistema de coordenadas fornecido.
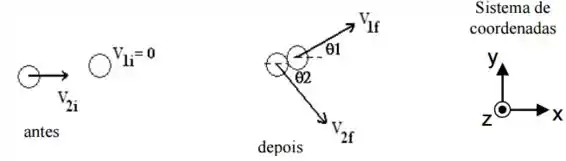
a) Ache o vetor velocidade de centro de massa dos discos antes da colisão.
b) Em termos dos vetores unitários e , determine o vetor velocidade do disco 1 após a colisão. Calcule o ângulo com que ele emerge.
c) A colisão é elástica ou não? Justifique com cálculos. Determine a razão entre as energias cinéticas depois e antes da colisão.d) Determine o vetor velocidade do centro de massa do sistema após a colisão, explicitamente usando seu resultado da letra . Compare com o resultado da letra e discuta.
Ver solução completaQuestão 13
Um homem de massa está na cesta de um balão de ar quente de massa , que se encontra a uma altura em relação ao solo. Devido a uma força de sustentação do ar conhecida como empuxo, o balão está em repouso em relação ao solo. O homem decide descer do balão usando uma escada de corda de suspensa que toca levemente o solo, conforme a figura.

a) Se o homem começar a descer pela escada com velocidade (em relação ao balão), qual o sentido e qual a velocidade com que o balão irá se mover em relação ao solo?
b) Após descer os até o final da escada, o balão terá subido e o homem se encontrará a uma distância entre a base da escada e o solo. Calcule o valor da distância .
Ver solução completaQuestão 14
Calculadoras científicas simples são autorizadas.
Eduardo e Mônica resolvem fazer um romântico passeio de canoa. Eduardo, com , senta-se em um extremo da canoa, enquanto Mônica, com , senta-se no outro extremo. A ponta em que está sentado Eduardo dista de da margem. O barco tem um comprimento total de e massa de . Quebrando o romantismo, Eduardo se dá conta de que esqueceu os remos na margem e tem a seguinte ideia: se eles trocam de lugar, o barco deverá se mover em direção à margem e com isto Mônica pode tentar alcançar os remos. Para não perderem o equilíbrio, primeiro caminhou Mônica, depois Eduardo.
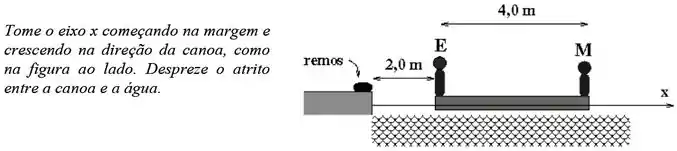
a) Durante o deslocamento de Mônica, a canoa tem uma velocidade escalar de em relação à água. Qual é a velocidade de Mônica, também em relação à água?
b) O braço de Mônica tem 60 cm. Ao final do deslocamento de ambos, ela consegue alcançar os remos? (despreze a variação do centro de massa de Mônica ao esticar um braço)
Justifique claramente o desenvolvimento em ambos itens!
Ver solução completaQuestão 15
Um homem pesando está parado sobre um vagão que pesa . O vagão está em repouso sobre os trilhos horizontais sem atrito. Se o homem começa a andar sobre o vagão com uma velocidade de , então após seu deslocamento em relação ao chão será:
A.
B.
C.
D.
E.
Ver solução completaQuestão 16
Sobre uma mesa horizontal perfeitamente lisa repousa um sistema formado por duas pequenas massas e , ligadas por uma mola de massa desprezível e que se encontra relaxada. A partir do instante passa a atuar sobre a massa uma força externa constante paralela à mesa, e uma força sobre a massa . Pode-se afirmar que para
- O centro de massa do sistema se move ao longo de uma reta
- O momento linear total do sistema se conserva
- A velocidade do centro de massa é uma função quadrática do tempo
- A distância entre as massas e permanece constante
- O momento angular total do sistema, referido ao centro de massa, permanece constante
Questão 17
Três pequenos discos de massas , e estão ligados por barras ideais (rígidas) de massas desprezíveis. Este sistema está apoiado sobre uma mesa horizontal lisa. Em um dado instante aplicam-se duas forças, e , sobre os discos de massas e , respectivamente. As forças são paralelas ao plano da mesa como mostra a figura (mesa vista de cima). No instante considerado a aceleração do centro de massa do sistema constituído pelos discos e pelas barras é:
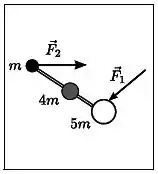
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h) O centro de massa permanece em repouso.
Ver solução completaQuestão 18
Um homem de massa está em pé sobre uma das extremidades de uma prancha que flutua num lago de águas calmas. A massa da prancha, que é distribuída de maneira uniforme em seu comprimento , é . O homem começa a andar em direção à outra extremidade da prancha. Desprezando o atrito entre água e a prancha, determine a distância que a prancha percorre durante o percurso do homem de uma extremidade à outra da prancha.
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 19
Duas pessoas, de mesma massa , estão de pé e presas às extremidades opostas de uma prancha, de comprimento e massa desprezível, que inicialmente se encontra em repouso sobre uma pista de gelo, como mostrado na figura. A pessoa da direita joga, com certa velocidade horizontal, uma bola de massa em direção à outra pessoa que consegue pegá-la. Despreze os efeitos da resistência do ar e do atrito entre a prancha e a pista de gelo. Para um observador parado na borda da pista:
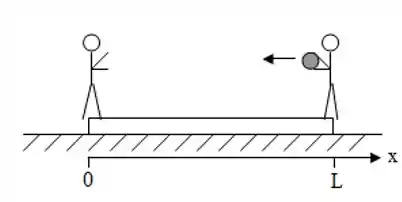
(a) Encontre a equação que descreve a posição do centro de massa () do conjunto prancha + pessoas + bola enquanto a bola vai da direita para a esquerda. Justifique sua resposta com argumentos físicos.
(b) Encontre as equações da velocidade e da posição do centro da prancha (que inicialmente vale ) enquanto a bola vai da direita para a esquerda, em função das massas e da velocidade da bola.
(c) Determine a posição da pessoa da direita, no momento em que a bola é agarrada pela pessoa da esquerda, usando o referencial da figura.
(d) O que acontece com o conjunto prancha + pessoas + bola após que a pessoa da esquerda agarrou a bola? Justifique sua resposta com argumentos físicos.
Ver solução completaQuestão 20
Um sistema é constituído por duas partículas de massas e , presas às extremidades de uma mola de constante elástica . O sistema está inicialmente em repouso em uma mesa horizontal sem atrito e a mola encontra-se na sua posição natural, como mostrado na figura. No instante começam a atuar duas forças constantes de mesmo módulo como indicado na figura. Utilizando os unitários relativos ao sistema de eixos indicado na figura determine:
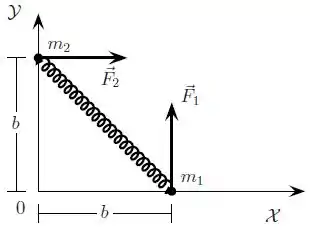
a) O vetor posição do centro de massa do sistema quando este se encontra em repouso.
b) O vetor posição do centro de massa para um instante posterior a .
Ver solução completaQuestão 21
Um homem de massa M/5 está em pé sobre uma das extremidades de uma prancha que repousa sobre a superfície de uma lago congelado. A massa da prancha, que é distribuída de maneira uniforme em seu comprimento L, é M. O homem começa a andar em direção à outra extremidade da prancha. Desprezando o atrito entre o gelo e a prancha, determine a distância D que a prancha percorre ao fim do percurso do homem de uma extremidade à outra da prancha.
a)
b)
c)
d)
e)
f)
Ver solução completaQuestão 22
Um bloco de massa está em repouso em um plano horizontal sem atrito quando é atingido por uma bala de massa que se deslocava com velocidade . A bala atinge o bloco e o atravessa, emergindo com velocidade . Desconsidere a perda de massa do bloco, bem como quaisquer efeitos gravitacionais.
(a) Qual é a velocidade do bloco depois que a bala o atravessa?
(b) Quanta energia foi dissipada na colisão?
(c) Qual é a variação na velocidade do centro de massa no evento acima?
Ver solução completaQuestão 23
Duas partículas de mesma massa estão ligadas por uma corda de massa desprezível. Uma das partículas é lançada para cima com velocidade , enquanto a outra está em repouso no chão. É correto afirmar sobre o centro de massa desta distribuição:
descreve uma trajetória com aceleração para baixo, mesmo enquanto uma das massas ainda está em contato com o chão.
descreve uma trajetória com aceleração para baixo a partir do momento que as duas bolas perdem o contato com o chão, com exceção dos momentos em que a corda está tensionada.
descreve uma trajetória com aceleração para baixo a partir do momento que as duas bolas perdem o contato com o chão.
descreve uma trajetória com aceleração menor que , para baixo a partir do momento que as duas bolas perdem o contato com o chão.
não é possível calcular a aceleração do centro de massa sem descrever a força de tensão da corda.
Ver solução completaQuestão 24
Dois blocos de massas iguais deslizam sobre uma superfície horizontal de maneira que o atrito entre eles e a superfície é desprezível. O movimento acontece na presença do campo gravitacional terrestre. Os módulos das velocidades iniciais dos blocos são tais que . O bloco carrega consigo uma mola (ver figura abaixo) de constante elástica cuja massa é desprezível.
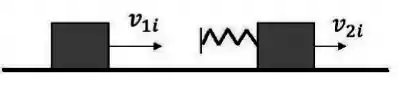
No referencial em que o centro de massa está em repouso, é incorreto afirmar que:
a energia mecânica é menor que no referencial original
os dois blocos estão em repouso no instante da compressão máxima
a energia potencial é menor que no referencial original
o momento linear total é zero
o momento linear dos blocos tem o mesmo módulo mas sentido contrário
Ver solução completaQuestão 25
Felipe e Bruna estão parados sobre uma plataforma plana. Felipe de massa 70 kg se encontra em uma extremidade que coincide com a origem enquanto Bruna de massa 55 kg se encontra na extremidade oposta a uma distância de 3,0 m de Felipe. A plataforma possui massa de 100 kg e pode se deslocar livre de atrito.

- Encontre a posição do centro de massa do sistema Felipe-Bruna-Plataforma ao longo do eixo x em relação à origem.
- Felipe e Bruna caminham sobre a plataforma em direções oposta até trocarem de lugar. No final desta troca de lugar, a plataforma se desloca d com relação à origem, encontre este deslocamento d.
Questão 26
(Cap 9 – Ex 98) Um homem de , que estava em um carrinho de golfe de que se movia a uma velocidade de , pulou do carrinho com velocidade horizontal nula em relação ao chão. Qual foi a variação da velocidade do carrinho, incluindo o sinal?
Ver solução completaQuestão 27
As quatro partículas, cujas velocidades são mostradas na figura, têm a mesma massa e movem-se com a mesma rapidez constante.
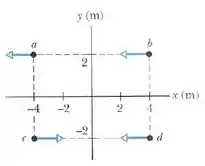
O seguinte par de partículas forma um sistema cujo centro de massa permanece em repouso na origem:
(A) a e b
(B) a e c
(C) b e c
(D) a e d
(E) b e d
Ver solução completaQuestão 28
(Cap 9 – Ex 98) Dois blocos de massas e estão ligados por uma mola e repousam em uma superfície sem atrito. Os blocos começam a se mover um em direção ao outro de modo que o bloco de viaja inicialmente a em direção ao centro de massa, que permanece em repouso. Qual é a velocidade inicial do outro bloco?
Ver solução completaQuestão 29
Duas partículas inicialmente separadas sofrem uma colisão totalmente inelástica na ausência de forças externas. Pode-se afirmar, sobre o sistema constituído pelas duas partículas, que
- A energia cinética do centro de massa do sistema é a mesma antes e depois da colisão;
- O módulo da velocidade do centro de massa do sistema é menor antes do que depois da colisão;
- A energia cinética total do sistema é a mesma antes e depois da colisão;
- O módulo da velocidade do centro de massa do sistema é maior antes do que depois da colisão;
- A energia cinética total do sistema é menor antes do que depois da colisão.
Questão 30
Uma partícula em repouso está sobre uma mesa horizontal com atrito desprezível e cujo centro de massa coincide com a origem de coordenadas . No instante ela explode em três partículas menores. A partícula 1 se afasta da origem de coordenadas com um momento linear . A partícula 2 se afasta da origem com um momento linear .
a) Determine o momento linear da partícula 3 e o ângulo que ele faz em relação ao eixo 𝑥 positivo.
b) Sabendo que a explosão dura , calcule as forças responsáveis pela explosão e mostre que durante este processo .
c) Calcule a posição do centro de massa do sistema após a explosão.
Ver solução completaQuestão 31
Um bloco deslocando-se com momento linear , colide com um bloco de momento linear , onde é constante. Suponha que não há força externa. Após a colisão o centro de massa do sistema segue, de acordo com o sistema de coordenadas ortogonais e os respectivos vetories unitários , e :
- na direção e sentido negativo;
- na direção e sentido negativo;
- na direção e sentido positivo;
- na direção e sentido positivo;
- em uma direção formando um ângulo com os eixos e .
Questão 32
Um sistema é composto por duas partículas que se movimentam em um plano horizontal . Em um dado instante , observa-se que as duas partículas, de massas e , partem da origem do sistema de coordenadas, com velocidades e , respectivamente. Sabendo-se que elas estão sujeitas somente a forças internas, o módulo do vetor posição do centro de massa (em metros) quando é:
Ver solução completaQuestão 33
Uma partícula de massa desloca-se sobre uma mesa horizontal, sem atrito, com velocidade . Num certo instante ela se desintegra espontaneamente em três fragmentos de massas , e com velocidades , e , com na mesma direção e sentido oposto a e perpendicular a e como mostrado na figura abaixo. O módulo da velocidade do fragmento de massa é . Em termos dos dados do problema, e , e utilizando o sistema de eixos da figura determine:
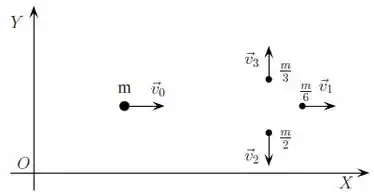
a) Os vetores velocidade e .
b) Os vetores velocidade dos fragmentos em relação ao referencial do centro de massa do sistema.
Ver solução completaQuestão 34
Um pescador de massa está sobre de um barco de massa . Ambos estão inicialmente em repouso. A extremidade do barco mais próxima da margem está a uma distância de da mesma. Assumindo que inicialmente o pescador está exatamente em cima do centro de massa do barco, qual é a distância mínima que ele deve caminhar em relação ao barco para que o barco toque a margem?
(a) na direção da margem, se aproximando da mesma;
(b) na direção da margem, se afastando da mesma;
(c) na direção da margem, se aproximando da mesma;
(d) na direção da margem, se afastando da mesma;
(e) na direção da margem, se aproximando da mesma;
(f) na direção da margem, se afastando da mesma;
(g) na direção da margem, se aproximando da mesma;
(h) na direção da margem, se afastando da mesma.
Ver solução completaQuestão 35
Dois pequenos discos, de massas e , se deslocam sobre uma mesa horizontal de coeficiente de atrito cinético com os discos . Inicialmente os discos possuem velocidades em direções perpendiculares cujos módulos são desconhecidos. Em um certo instante os discos colidem e passam a se deslocar juntos. Após a colisão o sistema se movimenta em uma direção que faz um ângulo com o eixo conforme a figura. Além disso observa-se que o sistema entra em repouso após percorrer uma distância desde o ponto onde ocorreu a colisão. Desprezando efeitos de rotação de cada disco, determine:
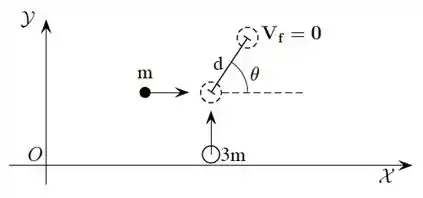
(b) Os vetores velocidade de cada disco no instante imediatamente anterior à colisão ocorrer.
(c) O vetor velocidade do centro de massa do sistema formado pelos discos no instante imediatamente anterior à colisão ocorrer.
Ver solução completaQuestão 36
Seja a colisão entre uma esfera de massa , cujo vetor posição é dado por e outra esfera de massa e vetor posição é dado por Imediatamente após a colisão, a esfera adquire uma velocidade de módulo e faz um ângulo de em relação ao eixo positivo. Considere o sistema isolado. Justifique suas respostas.
(a) Dado que o momento total do sistema imediatamente antes da colisão é , determine a velocidade do centro de massa imediatamente após a colisão.
(b) Determine a velocidade da esfera A imediatamente após a colisão.
(c) Determine se a colisão foi elástica ou inelástica.
Ver solução completaQuestão 37
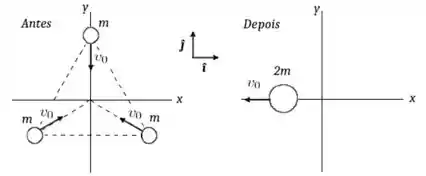
Três átomos idênticos de massa se deslocam no plano horizontal com velocidade de mesmo módulo , de tal forma que os três colidem num determinado ponto. Antes da colisão, os átomos encontram-se sempre equidistantes um do outro conforme mostra a figura. Após a colisão, verifica-se que dois dos átomos formam uma molécula de massa , que se move ao longo do sentido negativo do eixo , com uma velocidade de modulo . O terceiro átomo move-se isoladamente após a colisão. Responda as questões abaixo usando como dados e .
A) Mostre que a velocidade do centro de massa do sistema formado pelos três átomos é nula.
B) Calcule o vetor velocidade do terceiro átomo após a colisão no sistema de coordenadas indicado na figura.
C) Calcule a variação da energia cinética do sistema devido à colisão.
Questão 38
Uma bomba em repouso explode no espaço e se parte num grande número de pequenos fragmentos. No local da explosão a força gravitacional é zero. Qual das seguintes afirmações sobre esse evento é verdadeira?
(a) A energia cinética é conservada no processo
(b) A soma das energias cinéticas dos fragmentos é necessariamente zero
(c) Todos os fragmentos têm necessariamente a mesma energia cinética
(d) O centro de massa do sistema permanece em repouso após a explosão
(e) As massas dos fragmentos devem ser iguais entre si
Ver solução completa